题目内容
1．若tan（θ+$\frac{π}{4}$）=$\frac{1}{2}$，则tanθ=$-\frac{1}{3}$．分析 利用两角和的正切函数公式及特殊角的三角函数值即可得解．
解答 解：∵tan（θ+$\frac{π}{4}$）=$\frac{tanθ+tan\frac{π}{4}}{1-tanθtan\frac{π}{4}}$=$\frac{1+tanθ}{1-tanθ}$=$\frac{1}{2}$，
∴解得：tan$θ=-\frac{1}{3}$．
故答案为：$-\frac{1}{3}$．
点评 本题主要考查了两角和的正切函数公式及特殊角的三角函数值在化简求值中的应用，熟练掌握公式是解题的关键，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．
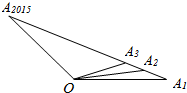如图，O为直线A1A2015外一点，若A1，A2，A3，A4，A5…A2015中任意相邻两点的距离相等，设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$，$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$，用$\overrightarrow{a}，\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$，其结果为（ ）
如图，O为直线A1A2015外一点，若A1，A2，A3，A4，A5…A2015中任意相邻两点的距离相等，设${\overrightarrow{OA}}_{1}=\overrightarrow{a}$，$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$，用$\overrightarrow{a}，\overrightarrow{b}$表示$\overrightarrow{O{A}_{1}}+\overrightarrow{O{A}_{2}}+…+\overrightarrow{O{A}_{2015}}$，其结果为（ ）| A． | 2014（$\overrightarrow{a}+\overrightarrow{b}$） | B． | 2015（$\overrightarrow{a}+\overrightarrow{b}$） | C． | $\frac{2014}{2}$（$\overrightarrow{a}+\overrightarrow{b}$） | D． | $\frac{2015}{2}$（$\overrightarrow{a}+\overrightarrow{b}$） |
12．复数z满足（1+i）z=2i（i为虚数单位），则z在复平面内对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
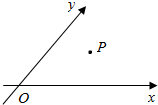如图，设α∈（0，π）且$α≠\frac{π}{2}$，当∠xOy=α时，定义平面坐标系xOy为斜坐标系，在斜坐标系中，任意一点P的斜坐标这样定义：e1，e2分别为x轴、y轴正方向相同的单位向量，若$\overrightarrow{OP}=x{e_1}+y{e_2}$，则记为$\overrightarrow{OP}=（x，y）$，那么在以下的结论中，正确的有（2）（4）（填上所有正确结论的序号）．
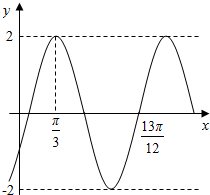已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$，x∈R）的部分图象如图所示．