题目内容
2．直三棱柱ABC-A1B1C1中，底面边长和侧棱长都等于2，D是BC的中点，则三棱锥A-B1DC1的体积为$\frac{2\sqrt{3}}{3}$．分析 画出图象，利用已知条件求出棱锥的底面积以及高，即可求解三棱锥A-B1DC1的体积．
解答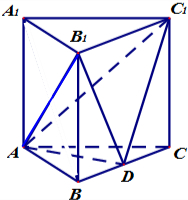 
解：由题意几何体的图形如图：所求三棱锥的体积，就是底面积为一个侧面面积的一半，棱锥的高为AD，
底面面积为：$\frac{1}{2}×2×2$=2，
高：$\sqrt{3}$，
三角锥的体积为：$\frac{1}{3}×2×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$．
故答案为：$\frac{2\sqrt{3}}{3}$．
点评 本题考查三棱柱与三棱锥的关系，棱锥的体积的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
如图，四棱锥P-ABCD的底面ABCD是平行四边形，PA⊥底面ABCD，∠PCD=90°，PA=AB=AC．
如图，在正三棱柱ABC-A1B1C1中（底面为正三角形且侧棱垂直于底面的三棱柱叫正三棱柱），各棱长都是4，D是BC的中点．
如图，AB⊥平面BCD，AB=BC=CD=1，AD与平面BCD成45°的角，
如图，在直角梯形ABCD中，AB∥CD，∠DAB=90°，AD=DC=$\frac{1}{2}$AB=1．直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到，且平面ABEF⊥平面ABCD．