题目内容
14. 如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=DC=$\frac{1}{2}$AB=1.直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD.
如图,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=DC=$\frac{1}{2}$AB=1.直角梯形ABEF可以通过直角梯形ABCD以直线AB为轴旋转得到,且平面ABEF⊥平面ABCD.(Ⅰ)求证:FA⊥BC;
(Ⅱ)求直线BD和平面BCE所成角的正弦值;
(Ⅲ)设H为BD的中点,M,N分别为线段FD,AD上的点(都不与点D重合).若直线FD⊥平面MNH,求MH的长.
分析 (Ⅰ)利用平面与平面垂直的性质证明:FA⊥平面ABCD,即可证明FA⊥BC;
(Ⅱ)以A为原点建立空间直角坐标系,求出平面BCE的一个法向量,利用向量的夹角公式,即可求直线BD和平面BCE所成角的正弦值;
(Ⅲ)设$\frac{DM}{DF}$=k(0<k≤1),则M(1-k,0,k),利用FD⊥平面MNH,求出M的坐标,即可求MH的长.
解答 (Ⅰ)证明:由已知得∠FAB=90°,所以FA⊥AB.
因为平面ABEF⊥平面ABCD,
且平面ABEF∩平面ABCD=AB,
所以FA⊥平面ABCD,
由于BC?平面ABCD,所以FA⊥BC.
(Ⅱ)解:由(Ⅰ)知FA⊥平面ABCD,所以FA⊥AB,FA⊥AD.
由已知DA⊥AB,所以AD,AB,AF两两垂直.
以A为原点建立空间直角坐标系(如图).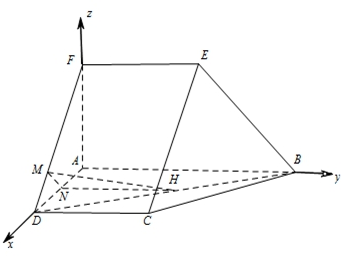
因为AD=DC=$\frac{1}{2}$AB=1,
则B(0,2,0),C(1,1,0),D(1,0,0),E(0,1,1),
所以$\overrightarrow{BC}$=(1,-1,0),$\overrightarrow{BE}$=(0,-1,1),
设平面BCE的一个法向量$\overrightarrow{n}$=(x,y,z).
所以$\left\{\begin{array}{l}{x-y=0}\\{-y+z=0}\end{array}\right.$.
令x=1,则$\overrightarrow{n}$=(1,1,1).
设直线BD与平面BCE所成角为θ,
因为$\overrightarrow{BD}$=(1,-2,0),
所以sinθ=|$\frac{1-2}{\sqrt{3}•\sqrt{5}}$|=$\frac{\sqrt{15}}{15}$.
所以直线BD和平面BCE所成角的正弦值为$\frac{\sqrt{15}}{15}$.
(Ⅲ)解:A(0,0,0),D(1,0,0),F(0,0,1),B(0,2,0),H($\frac{1}{2}$,1,0).
设$\frac{DM}{DF}$=k(0<k≤1),则M(1-k,0,k),
∴$\overrightarrow{MH}$=(k-$\frac{1}{2}$,1,-k),$\overrightarrow{FD}$=(1,0,-1).
若FD⊥平面MNH,则FD⊥MH.
即$\overrightarrow{FD}•\overrightarrow{MH}$=0.
∴k-$\frac{1}{2}$+k=0.解得k=$\frac{1}{4}$.
则$\overrightarrow{MH}$=($\frac{1}{4}$,1,-$\frac{1}{4}$),|$\overrightarrow{MH}$|=$\frac{3}{4}\sqrt{2}$.
点评 本题考查线面垂直的判定、平面与平面垂直的性质,考查线面角,正确运用向量法是关键.

| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
 如图,已知直三棱锥ABC-A1B1C1中,AC=BC=2,且AC⊥BC,点D是A1B1中点.
如图,已知直三棱锥ABC-A1B1C1中,AC=BC=2,且AC⊥BC,点D是A1B1中点. 如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,分别为CD、PB的中点,AE=$\sqrt{3}$.
如图,四棱锥P-ABCD的底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,分别为CD、PB的中点,AE=$\sqrt{3}$.