题目内容
12. 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC.(I)求证:AC⊥CD;
(Ⅱ)点E在棱PC上,满足∠DAE=60°,求二面角B-AE-D的余弦值.
分析 (Ⅰ)通过线面垂直的判定定理及性质定理即得结论;
(Ⅱ)以点A为原点,以$\overrightarrow{AB}$为x轴正方向、以|$\overrightarrow{AB}$|为单位长度,建立空间直角坐标系.利用∠DAE=60°即cos<$\overrightarrow{AE}$,$\overrightarrow{AD}$>=$\frac{1}{2}$可得$\overrightarrow{AE}$=(0,$\frac{1}{2}$,$\frac{1}{2}$),通过cos<$\overrightarrow{AB}$,$\overrightarrow{ED}$>=$\frac{\overrightarrow{AB}•\overrightarrow{ED}}{|\overrightarrow{AB}||\overrightarrow{ED}|}$即得二面角B-AE-D的余弦值.
解答 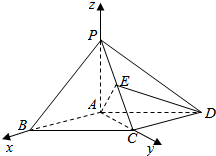 (Ⅰ)证明:因为PA⊥底面ABCD,所以PA⊥CD,
(Ⅰ)证明:因为PA⊥底面ABCD,所以PA⊥CD,
因为∠PCD=90°,所以PC⊥CD,
所以CD⊥平面PAC,所以CD⊥AC;
(Ⅱ)解:∵底面ABCD是平行四边形,CD⊥AC,∴AB⊥AC.
又PA⊥底面ABCD,∴AB,AC,AP两两垂直.
如图所示,以点A为原点,以$\overrightarrow{AB}$为x轴正方向、以|$\overrightarrow{AB}$|为单位长度,建立空间直角坐标系.
则B(1,0,0),C(0,1,0),P(0,0,1),D(-1,1,0).
设$\overrightarrow{PE}$=λ$\overrightarrow{PC}$=λ(0,1,-1),则$\overrightarrow{AE}$=$\overrightarrow{AP}$+$\overrightarrow{PE}$=(0,λ,1-λ),
又∠DAE=60°,则cos<$\overrightarrow{AE}$,$\overrightarrow{AD}$>=$\frac{1}{2}$,
即$\frac{λ}{\sqrt{2}\sqrt{2{λ}^{2}-2λ+1}}$=$\frac{1}{2}$,解得λ=$\frac{1}{2}$.
则$\overrightarrow{AE}$=(0,$\frac{1}{2}$,$\frac{1}{2}$),$\overrightarrow{ED}$=$\overrightarrow{AD}$-$\overrightarrow{AE}$=(-1,$\frac{1}{2}$,-$\frac{1}{2}$),
所以cos<$\overrightarrow{AB}$,$\overrightarrow{ED}$>=$\frac{\overrightarrow{AB}•\overrightarrow{ED}}{|\overrightarrow{AB}||\overrightarrow{ED}|}$=-$\frac{\sqrt{6}}{3}$.
因为$\overrightarrow{AE}$•$\overrightarrow{ED}$=0,所以$\overrightarrow{AE}$⊥$\overrightarrow{ED}$.
又$\overrightarrow{AB}$⊥$\overrightarrow{AE}$,故二面角B-AE-D的余弦值为-$\frac{\sqrt{6}}{3}$.
点评 本题考查空间中线线垂直的判定,以及求二面角的三角函数值,注意解题方法的积累,属于中档题.

| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
 如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°DC=2AB=2a,DA=$\sqrt{3}$A,PD=$\sqrt{3}$a,E为BC中点,连结AE,交BD于O.
如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°DC=2AB=2a,DA=$\sqrt{3}$A,PD=$\sqrt{3}$a,E为BC中点,连结AE,交BD于O.