题目内容
7．某几何体的三视图如图所示，则该几何体外接球表面积为8π．
分析 由几何体的三视图还原为几何体，然后求出其外接球的半径，最后求表面积．
解答 解：三视图对应的几何体如图P-ABCD，是长宽高分别是2，$\frac{3}{2}$，$\sqrt{3}$的长方体中的四棱锥，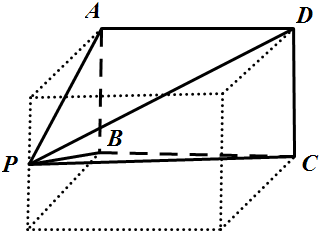
所以其外接球的半径为$\sqrt{（\frac{\sqrt{3}}{6}•\sqrt{3}）^{2}+1+（\frac{\sqrt{3}}{2}）^{2}}$
=$\sqrt{2}$，
所以外接球半径为$\sqrt{2}$，
所以球的表面积为4π（$\sqrt{2}$）2=8π；
故答案为：8π．
点评 本题考查了由几何体的三视图还原几何体以及求几何体的外接球表面积；关键是还原几何体．
练习册系列答案
相关题目
如图，在多面体ABC-A1B1C1中，四边形ABB1A1是正方形，△A1CB是等边三角形，AC=AB=1，B1C1∥BC，BC=2B1C1．
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，左右焦点分别为F1、F2，点A（2，$\sqrt{3}$），点F2在线段AF1的中垂线上．