题目内容
5.证明:$\frac{2}{1}+\frac{3}{2}+\frac{4}{3}+…+\frac{n+1}{n}>n•\root{n}{n+1}$.分析 由均值不等式$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$≥$\root{n}{{a}_{1}•{a}_{2}…{a}_{n}}$(a1,a2,…,an>0),当且仅当a1=a2=…=an取得等号.即可得证.
解答 证明:由均值不等式$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$≥$\root{n}{{a}_{1}•{a}_{2}…{a}_{n}}$
(a1,a2,…,an>0),当且仅当a1=a2=…=an取得等号.
可得$\frac{2}{1}$+$\frac{3}{2}$+$\frac{4}{3}$+…+$\frac{n+1}{n}$≥n•$\root{n}{\frac{2}{1}•\frac{3}{2}•\frac{4}{3}…\frac{n+1}{n}}$=n•$\root{n}{n+1}$.
由于$\frac{2}{1}$,$\frac{3}{2}$,$\frac{4}{3}$,…,$\frac{n+1}{n}$不相等,
则有$\frac{2}{1}+\frac{3}{2}+\frac{4}{3}+…+\frac{n+1}{n}>n•\root{n}{n+1}$成立.
点评 本题考查均值不等式的运用,考查运算化简能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知回归直线方程中斜率的估计值为1.23,样本点的中心(5,6.2),则回归直线方程为( )
| A. | y=1.23x-0.05 | B. | y=1.23x+0.05 | C. | y=1.23x+6.2 | D. | y=1.23x+5 |
10.某程序框图如图所示,若其输出结果是56,则判断框中应填写的是( )
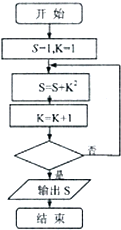

| A. | K<4 | B. | K<5 | C. | K<6 | D. | K<7 |