题目内容
已知a,b,c是非零实数,则“a,b,c成等比数列”是“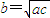 ”的 条件(从“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中选择一个填空).
”的 条件(从“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中选择一个填空).
【答案】分析:由a,b,c成等比数列可得 b=±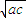 ,不能推出
,不能推出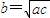 .但由
.但由 ,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.由此得出结论.
,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.由此得出结论.
解答:解:由a,b,c成等比数列可得 b=±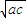 ,不能推出
,不能推出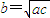 .
.
但由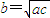 ,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.
,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.
故“a,b,c成等比数列”是“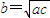 ”的必要不充分条件,
”的必要不充分条件,
故答案为 必要不充分.
点评:本题主要考查充分条件、必要条件、充要条件的定义,等比数列的定义和性质,属于中档题.
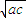 ,不能推出
,不能推出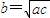 .但由
.但由 ,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.由此得出结论.
,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.由此得出结论.解答:解:由a,b,c成等比数列可得 b=±
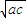 ,不能推出
,不能推出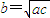 .
.但由
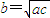 ,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.
,a,b,c是非零实数,可得 b2=ac,a,b,c成等比数列.故“a,b,c成等比数列”是“
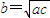 ”的必要不充分条件,
”的必要不充分条件,故答案为 必要不充分.
点评:本题主要考查充分条件、必要条件、充要条件的定义,等比数列的定义和性质,属于中档题.

练习册系列答案
相关题目