题目内容
已知
,
,
是非零平面向量,且
与
不共线,则方程
x2+
x+
=
的解的情况是( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| 0 |
分析:先将向量
移到另一侧得到关于向量
=-
x2-
x,再由平面向量的基本定理判断解的情况即可.
| c |
| c |
| a |
| b |
解答:解:∵
x2+
x+
=
∴
=-
x2-
x,
因为
可以由不共线的向量唯一表示,
所以可以由
和
唯一表示,
若恰好在基向量下的分解的系数是乘方的关系,则有一个解,否则无解,
所以至多一个解.
故选A.
| a |
| b |
| c |
| 0 |
∴
| c |
| a |
| b |
因为
| c |
所以可以由
| a |
| b |
若恰好在基向量下的分解的系数是乘方的关系,则有一个解,否则无解,
所以至多一个解.
故选A.
点评:本题主要考查平面向量的基本定理,即平面内任意向量都可由两不共线的非零向量唯一表示出来.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
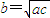 ”的 条件(从“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中选择一个填空).
”的 条件(从“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中选择一个填空).