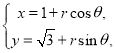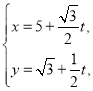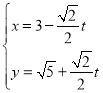题目内容
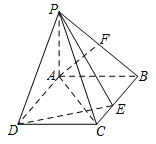
【题目】如图在三棱柱![]() 中,
中,![]() 为
为![]() 边的中点.
边的中点.![]() .
.
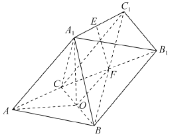
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 为
为![]() 中点且
中点且![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析(2)![]()
【解析】
![]() 由题意知,
由题意知,![]() ,利用线面平行的判定定理即可证明;
,利用线面平行的判定定理即可证明;
![]() 由已知条件可得,
由已知条件可得,![]() 由线面垂直的判定知,
由线面垂直的判定知,![]() 平面
平面![]() ,由线面垂直的性质知,
,由线面垂直的性质知,![]() ,由
,由![]() 知,
知,![]() ,进而证明
,进而证明![]() 平面
平面![]() ,由面面垂直的判定定理知,平面
,由面面垂直的判定定理知,平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,过
,过![]() 点作
点作![]() ,则
,则![]() 平面
平面![]() ,利用等体积法:
,利用等体积法:![]() 求解即可.
求解即可.
(1)证明:因为三棱柱![]() 中,侧面
中,侧面![]() 为平行四边形,
为平行四边形,
由![]() ,可知
,可知![]() 为
为![]() 的中点,又因为
的中点,又因为![]() 为
为![]() 边的中点,
边的中点,
所以![]() ,
,
因为![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)作图如下:
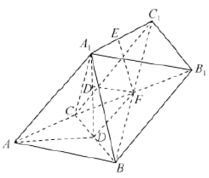
因为![]() ,
,![]() ,
,![]() 为公共边,
为公共边,
所以![]() ,所以
,所以![]() ,
,
因为![]() 为
为![]() 中点,
中点,![]() ,
,
则![]() ,
,![]() ,
,![]()
由线面垂直的判定知,![]() 平面
平面![]() ,
,
所以![]() ,
,
又因为![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,连
中点,连![]() ,
,
则![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
过![]() 点作
点作![]() ,则
,则![]() 平面
平面![]() ,
,
即![]() 为点
为点![]() 到平面
到平面![]() 的距离,
的距离,
因为![]() ,
,![]() ,
,
所以三角形![]() 为等边三角形,即
为等边三角形,即![]() ,
,
又![]() ,所以满足
,所以满足![]() ,
,
即![]() ,
,![]() ,
,
由![]() 知,
知,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案【题目】某企业响应省政府号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了![]() 件产品作为样本,检测一项质量指标值,若该项质量指标值落在
件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表
内的产品视为合格品,否则为不合格品.如图是设备改造前的样本的频率分布直方图,表![]() 是设备改造后的样本的频数分布表.
是设备改造后的样本的频数分布表.
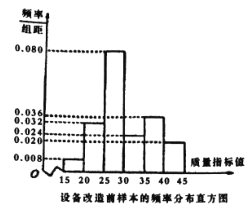
表:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据频率分布直方图和表 提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行登记细分,质量指标值落在![]() 内的定为一等品,每件售价
内的定为一等品,每件售价![]() 元;质量指标值落在
元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价
内的定为二等品,每件售价![]() 元;其它的合格品定为三等品,每件售价
元;其它的合格品定为三等品,每件售价![]() 元.根据表
元.根据表![]() 的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()