题目内容
已知函数y=sin2x+acos2x的图象关于直线 对称,则函数y=asin2x-cos2x的图象关于下列各点中对称的是( )
对称,则函数y=asin2x-cos2x的图象关于下列各点中对称的是( )A.(
 ,0)
,0)B.(
 ,0)
,0)C.(
 ,0)
,0)D.(
 ,0)
,0)
【答案】分析:利用辅助角公式化简函数的表达式为一个角的一个三角函数的形式,结合提交求出θ,然后化简函数y=asin2x-cos2x求出对称中心即可.
解答:解:函数y=sin2x+acos2x= sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线
sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线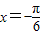 对称,所以θ=kπ+
对称,所以θ=kπ+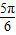 ,k∈Z,
,k∈Z,
则函数y=asin2x-cos2x=-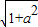 cos(2x+θ),显然x=
cos(2x+θ),显然x=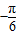 时,cos(2x+θ)=0,就是函数关于(
时,cos(2x+θ)=0,就是函数关于(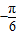 ,0)对称;
,0)对称;
故选B
点评:本题是基础题,考查三角函数的对称轴方程的应用,对称中心的求法,辅助角公式的应用,考查计算能力.
解答:解:函数y=sin2x+acos2x=
 sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线
sin(2x+θ),其中tanθ=a;已知函数y=sin2x+acos2x的图象关于直线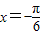 对称,所以θ=kπ+
对称,所以θ=kπ+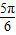 ,k∈Z,
,k∈Z,则函数y=asin2x-cos2x=-
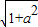 cos(2x+θ),显然x=
cos(2x+θ),显然x=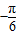 时,cos(2x+θ)=0,就是函数关于(
时,cos(2x+θ)=0,就是函数关于(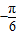 ,0)对称;
,0)对称;故选B
点评:本题是基础题,考查三角函数的对称轴方程的应用,对称中心的求法,辅助角公式的应用,考查计算能力.

练习册系列答案
相关题目



