题目内容
在平面直角坐标系xOy中,直线l:x+y+2=0在矩阵M= 对应的变换作用下得到直线m:x-y-4=0,求实数a、b的值.
对应的变换作用下得到直线m:x-y-4=0,求实数a、b的值.
 对应的变换作用下得到直线m:x-y-4=0,求实数a、b的值.
对应的变换作用下得到直线m:x-y-4=0,求实数a、b的值.a=2,b=3.
(解法1)在直线l:x+y+2=0上取两点A(-2,0),B(0,-2),A、B在矩阵M对应的变换作用下分别对应于点A′、B′,因为

= ,所以A′的坐标为(-2,-2b);
,所以A′的坐标为(-2,-2b);

 =
= ,所以B′的坐标为(-2a,-8).由题意A′、B′在直线m:x-y-4=0上,所以
,所以B′的坐标为(-2a,-8).由题意A′、B′在直线m:x-y-4=0上,所以 解得a=2,b=3.
解得a=2,b=3.
(解法2)设直线l:x+y+2=0上任意一点(x,y)在矩阵M对应的变换作用下对应于点(x′,y′).因为
 =
= ,所以x′=x+ay,y′=bx+4y.因为(x′,y′)在直线m上,所以(x+ay)-(bx+4y)-4=0,即(1-b)x+(a-4)y-4=0.
,所以x′=x+ay,y′=bx+4y.因为(x′,y′)在直线m上,所以(x+ay)-(bx+4y)-4=0,即(1-b)x+(a-4)y-4=0.
又点(x,y)在直线x+y+2=0上,所以 ,解得a=2,b=3
,解得a=2,b=3


=
 ,所以A′的坐标为(-2,-2b);
,所以A′的坐标为(-2,-2b);
 =
= ,所以B′的坐标为(-2a,-8).由题意A′、B′在直线m:x-y-4=0上,所以
,所以B′的坐标为(-2a,-8).由题意A′、B′在直线m:x-y-4=0上,所以 解得a=2,b=3.
解得a=2,b=3.(解法2)设直线l:x+y+2=0上任意一点(x,y)在矩阵M对应的变换作用下对应于点(x′,y′).因为

 =
= ,所以x′=x+ay,y′=bx+4y.因为(x′,y′)在直线m上,所以(x+ay)-(bx+4y)-4=0,即(1-b)x+(a-4)y-4=0.
,所以x′=x+ay,y′=bx+4y.因为(x′,y′)在直线m上,所以(x+ay)-(bx+4y)-4=0,即(1-b)x+(a-4)y-4=0.又点(x,y)在直线x+y+2=0上,所以
 ,解得a=2,b=3
,解得a=2,b=3
练习册系列答案
相关题目
 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成 ,求矩阵M。
,求矩阵M。 ,若矩阵M的逆矩阵M-1=
,若矩阵M的逆矩阵M-1= ,求a、b的值.
,求a、b的值.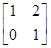 对应的变换作用下变为直线l′:x+by=1.
对应的变换作用下变为直线l′:x+by=1.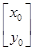 =
=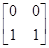 对应的变换作用下得到的图形.
对应的变换作用下得到的图形. 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .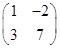 .
.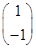 ,试求向量X.
,试求向量X.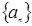 ,满足
,满足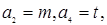 且
且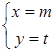 是增广矩阵
是增广矩阵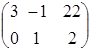 的线性方程组
的线性方程组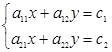 的解,则无穷等比数列
的解,则无穷等比数列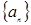 各项和的数值是 _________.
各项和的数值是 _________.