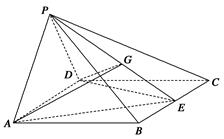
题目内容
如图,斜四棱柱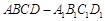 的底面
的底面 是矩形,平面
是矩形,平面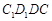 ⊥平面
⊥平面 ,
,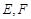 分别为
分别为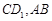 的中点.
的中点.
求证:
(1)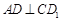 ;(2)
;(2)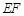 ∥平面
∥平面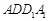 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)要证明线与线的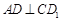 ,可以转化为证明线与面的
,可以转化为证明线与面的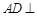 平面
平面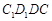 ,而由题目所给的平面
,而由题目所给的平面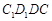 ⊥平面
⊥平面 利用面面垂直的性质定理可以得到.
利用面面垂直的性质定理可以得到.
(2)要证明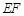 ∥平面
∥平面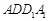 ,可以转化为线线平行,即通过添加辅助平面,在平面
,可以转化为线线平行,即通过添加辅助平面,在平面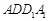 找一条直线与EF平行即可.
找一条直线与EF平行即可.
试题解析:证明:(1)由底面 为矩形得到
为矩形得到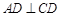 , 2分
, 2分
又∵平面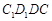 ⊥平面
⊥平面 ,平面
,平面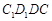
 平面
平面 平面=
平面=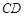 ,
,
∴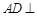 平面
平面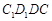 . 4分
. 4分
又∵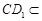 面
面 ,∴
,∴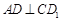 . 6分
. 6分
(2)设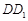 中点为
中点为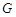 ,连结
,连结 ,
, .
.
∵ 分别为
分别为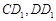 的中点,∴
的中点,∴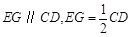 . 8分
. 8分
在矩形 中,由
中,由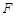 是
是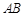 的中点,得到
的中点,得到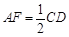 且
且 , 10分
, 10分
∴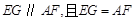 .
.
∴四边形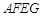 是平行四边形,∴
是平行四边形,∴ . 12分
. 12分
∵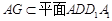 ,
, 平面
平面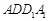 ,
,
∴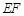 ∥平面
∥平面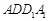 . 14分
. 14分
考点:(1)线线垂直的判定;(2)线面平行的判定.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目

 的值..
的值..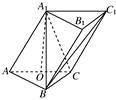
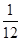 ·VABC-A1B1C1,求A1E的长度.
·VABC-A1B1C1,求A1E的长度. 中,
中, ,
, 平面
平面 ,且
,且 ,点
,点 是
是 的中点.
的中点.
 ;
; 的大小.
的大小.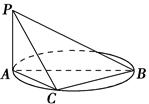
 EF.
EF.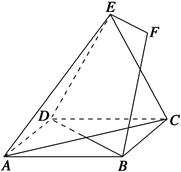
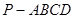 中,底面
中,底面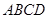 为矩形,
为矩形,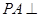 底面
底面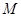 、
、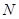 分别是
分别是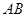 、
、 中点.
中点. 
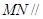 平面
平面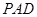 ;
; .
.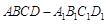 中,
中,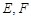 分别
分别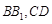 的中点.
的中点.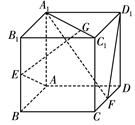
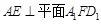 ;
;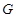 是靠近
是靠近 的
的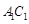 的四等分点,求证:
的四等分点,求证: .
.