题目内容
如图,在四棱锥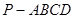 中,底面
中,底面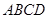 为矩形,
为矩形,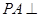 底面
底面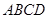 ,
,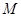 、
、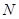 分别是
分别是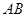 、
、 中点.
中点. 
(1)求证: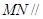 平面
平面 ;
;
(2)求证: .
.
(1)参考解析;(2)参考解析
解析试题分析:(1)要证直线与平面平行,根据直线与平面平行的判定定理,需要在平面内找一条直线与已知直线平行,由于本小题中点较多,所以想到作出四边形AMNQ.通过判定平行四边形,然后再用平行四边形的性质得到所需要的两直线平行,这种方法也是在证明直线与平面平行时的常用的方法.
(2)直线与直线垂直的证明根据判断定理,一般需要转化为证明直线与平面的垂直.这题是根据第一步的结论证明AB与平面PAD垂直,从而可得结论.
试题解析:证明:(1)取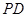 中点
中点 ,连结
,连结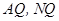 .
.
因为 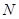 是
是 中点,
中点,
所以 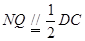 .
.
又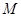 是
是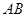 中点,
中点,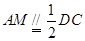 ,
,
所以 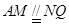 ,
,
四边形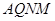 是平行四边形.所以
是平行四边形.所以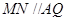 .因为
.因为 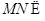 平面
平面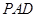 ,
,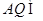 平面
平面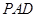 ,
,
所以 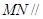 平面
平面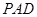 . 7分
. 7分
(2)因为 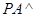 平面
平面 ,所以
,所以 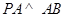 .
.
又  是矩形,
是矩形,
所以 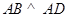 .
.
所以 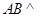 平面
平面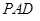 ,
,
所以 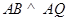 .又
.又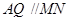 ,
,
所以 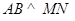 .
.
考点:1.直线与平面平行的判断定理.2.直线与直线垂直的判断方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 AD,BE∥=
AD,BE∥=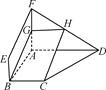
 的底面
的底面 是矩形,平面
是矩形,平面 ⊥平面
⊥平面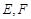 分别为
分别为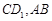 的中点.
的中点.
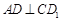 ;(2)
;(2)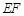 ∥平面
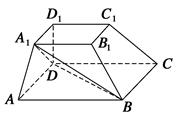
∥平面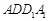 .
.
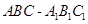 中,
中,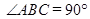 ,
,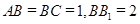 ,求:
,求: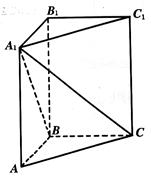
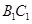 与
与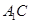 所成角的大小;
所成角的大小; 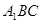 的距离.
的距离.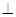 平面ABE,AE=EB=BC=2,F为CE上的点.且BF
平面ABE,AE=EB=BC=2,F为CE上的点.且BF 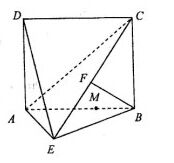
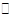 平面DAE.
平面DAE.  ,点F是PB的中点,点E在边BC上移动
,点F是PB的中点,点E在边BC上移动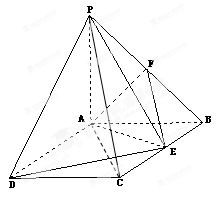
 中,
中, ,
,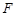 分别为
分别为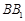 ,
,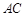 的中点.
的中点.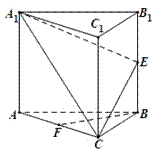
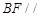 平面
平面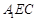 ;
;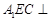 平面
平面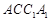 .
.