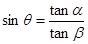题目内容
四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是边长为2的正方形,又PA=PD,∠APD=60°,E、G分别是BC、PE的中点.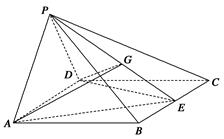
(1)求证:AD⊥PE;
(2)求二面角E-AD-G的正切值.
(1)AD⊥PE;(2)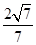 .
.
解析试题分析:(1)证明线线垂直要通过线面垂直证明,题中所给侧面PAD⊥底面ABCD是面面垂直,通过取AD的中点O,连结OP,OE,∵PA=PD,∴OP⊥AD,而OE⊥AD.,则AD⊥平面OPE.,从而能够证出AD⊥PE..(2)求二面角E-AD-G的正切值可以通过两种方法:①常规方法,作出二面角的平面角,并求出,取OE的中点F,连结FG,OG,则由(1)易知AD⊥OG,又OE⊥AD,∴∠GOE就是二面角E-AD-G的平面角,再利用三角形中边长关系求出∠GOE的正切值;②空间向量法,建立如图所示的空间直角坐标系,写出已知点的坐标,设平面ADG的法向量为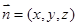 ,根据
,根据 ,求出
,求出
,而平面EAD的一个法向量为 ,再根据
,再根据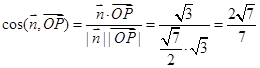 求出.
求出.
试题解析:(1)如图,取AD的中点O,连结OP,OE,∵PA=PD,∴OP⊥AD,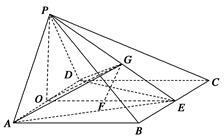
又E是BC的中点,∴OE∥AB,∴OE⊥AD.
又OP∩OE=0,∴AD⊥平面OPE.
∵PE?平面OPE,∴AD⊥PE.
(2)解法一:取OE的中点F,连结FG,OG,则由(1)易知AD⊥OG,
又OE⊥AD,∴∠GOE就是二面角E-AD-G的平面角,
∵PA=PD,∠APD=60°,
∴△APD为等边三角形,且边长为2,
∴OP=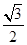 ×2=
×2= ,FG=
,FG= OP=
OP=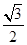 ,OF=
,OF= CD=1,
CD=1,
∴OG=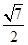 ,∴cos∠GOE=
,∴cos∠GOE=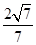
解法二:建立如图所示的空间直角坐标系,则A(1,0,0),D(-1,0,0),P(0,0, ),E(0,2,0),
),E(0,2,0),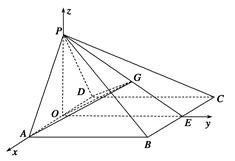
∴
设平面ADG的法向量为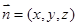 ,
,
由 得
得 ,
,
∴ .
.
又平面EAD的一个法向量为 ,
,
又因为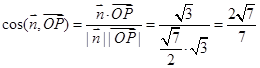 .
.
考点:1.线线垂直的证明;2.二面角的求解.

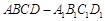 的底面
的底面 是矩形,平面
是矩形,平面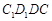 ⊥平面
⊥平面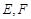 分别为
分别为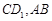 的中点.
的中点.
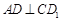 ;(2)
;(2)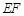 ∥平面
∥平面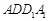 .
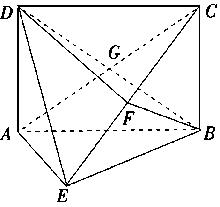
. ,点F是PB的中点,点E在边BC上移动
,点F是PB的中点,点E在边BC上移动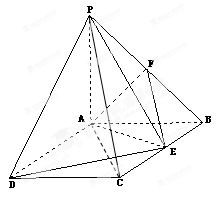
 中,
中, ,
,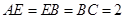 ,
,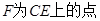 ,且
,且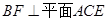 ,
,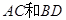 交于点
交于点 .
.
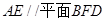 ;
;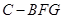 的体积.
的体积. 中,
中,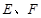 分别为
分别为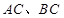 的中点.
的中点.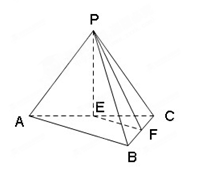
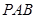 ;
;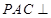 平面
平面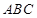 ,且
,且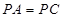 ,
,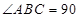 º,求证:平面
º,求证:平面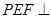 平面
平面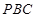
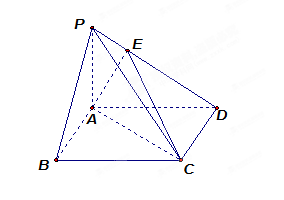
 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形,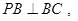
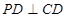 ,且
,且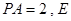 点满足
点满足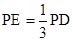 .
. 
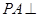 平面
平面 上是否存在点
上是否存在点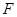 ,使得
,使得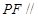 平面
平面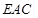 ?若存在,确定点
?若存在,确定点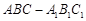 中,
中,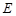 ,
,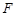 分别为
分别为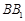 ,
,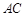 的中点.
的中点.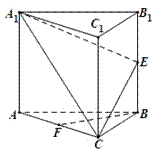
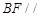 平面
平面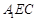 ;
;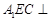 平面
平面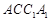 .
. 中,
中,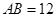 ,
,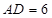 ,
,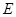 、
、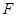 分别为
分别为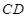 、
、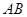 边上的点,且
边上的点,且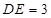 ,
,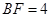 ,将
,将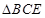 沿
沿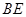 折起至
折起至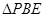 位置(如图2所示),连结
位置(如图2所示),连结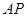 、
、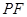 ,其中
,其中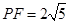 .
.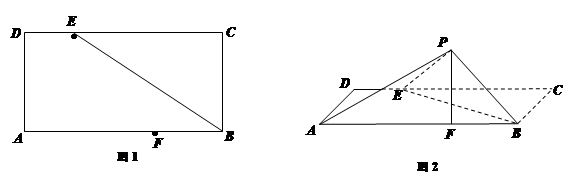
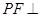 平面
平面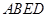 ;
;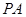 上是否存在点
上是否存在点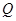 使得
使得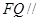 平面
平面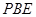 ?若存在,求出点
?若存在,求出点 到平面
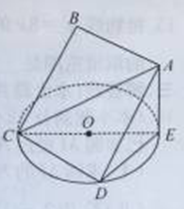
到平面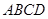 所在平面与圆
所在平面与圆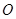 所在的平面相交于
所在的平面相交于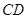 ,线段
,线段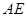 垂直于圆
垂直于圆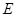 为圆
为圆 、
、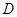 的点,设正方形
的点,设正方形 ,且
,且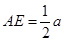 .
.
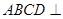 平面
平面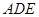 ;
;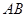 与
与 所成的角为
所成的角为 ,
,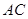 与底面
与底面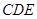 所成角为
所成角为 ,二面角
,二面角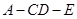 所成角为
所成角为 ,求证
,求证