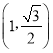题目内容
【题目】已知P是圆![]() 上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
上任意一点,F2(1,0),线段PF2的垂直平分线与半径PF1交于点Q,当点P在圆F1上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点![]() 的直线l与(1)中曲线相交于A,B两点,O为坐标原点,求△AOB面积的最大值及此时直线l的方程.
的直线l与(1)中曲线相交于A,B两点,O为坐标原点,求△AOB面积的最大值及此时直线l的方程.
【答案】(1)![]() .(2)
.(2)![]() 面积的最大值为
面积的最大值为![]() ,此时直线l的方程为
,此时直线l的方程为![]() .
.
【解析】
(1)根据垂直平分线的性质,利用椭圆定义法可求得曲线C的方程;
(2)设直线l的方程为x=ty![]() 与椭圆
与椭圆![]() 交于点A(x1,y1),B(x2,y2),联立直线与椭圆的方程消去x,利用韦达定理结合三角形的面积,利用换元法以及基本不等式求解最值,然后推出直线方程.
交于点A(x1,y1),B(x2,y2),联立直线与椭圆的方程消去x,利用韦达定理结合三角形的面积,利用换元法以及基本不等式求解最值,然后推出直线方程.
(1)由已知|QF1|+|QF2|=|QF1|+|QP|=|PF1|=4,
所以点Q的轨迹为以为![]() ,
,![]() 焦点,长轴长为4的椭圆,
焦点,长轴长为4的椭圆,
则2a=4且2c=2,所以a=2,c=1,则b2=3,
所以曲线C的方程为![]() ;
;
(2)设直线l的方程为x=ty![]() 与椭圆
与椭圆![]() 交于点A(x1,y1),B(x2,y2),
交于点A(x1,y1),B(x2,y2),
联立直线与椭圆的方程消去x,得(3t2+4)y2﹣6![]() ty﹣3=0,
ty﹣3=0,
则y1+y2![]() ,y1y2
,y1y2![]() ,
,
则S△AOB![]() |OM||y1﹣y2|
|OM||y1﹣y2|![]()
![]()
![]() ,
,
令![]() ,则u≥1,上式可化为
,则u≥1,上式可化为 ,
,
当且仅当u![]() ,即t=±
,即t=±![]() 时等号成立,
时等号成立,
因此△AOB面积的最大值为![]() ,此时直线l的方程为x=±
,此时直线l的方程为x=±![]() .
.

练习册系列答案
相关题目