Question

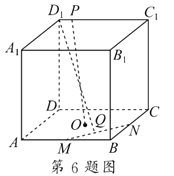
【题目】如图，正方形AMDE的边长为2，B，C分别为AM，MD的中点．在五棱锥P－ABCDE中，F为棱PE的中点，平面ABF与棱PD，PC分别交于点G，H.

(1)求证：AB∥FG；

(2)若PA⊥底面ABCDE，且PA＝AE.求直线BC与平面ABF所成角的大小，并求线段PH的长．

Answer 1

【答案】（1）详见解析（2）点H的坐标为()．PH＝2.

【解析】试题分析：（1）运用线面平行的判定定理和性质定理即可证得；（2）由于PA⊥底面ABCDE，底面AMDE为正方形，建立如图的空间直角坐标系Axyz，分别求出A，B，C，E，P，F，及向量BC的坐标，设平面ABF的法向量为n=（x，y，z），求出一个值，设直线BC与平面ABF所成的角为α，运用sinα=|cos＜n， ＞|，求出角α；设H（u，v，w），再设 (0＜λ＜1)，用λ表示H的坐标，再由n =0，求出λ和H的坐标，再运用空间两点的距离公式求出PH的长．

试题解析：

(1)在正方形AMDE中，因为B是AM的中点，所以AB∥DE.

又因为AB平面PDE，所以AB∥平面PDE.

因为AB平面ABF，且平面ABF∩平面PDE＝FC，

所以AB∥FG.

(2)因为PA⊥底面ABCDE，所以PA⊥AB，PA⊥AE.

如图建立空间直角坐标系A－xyz，

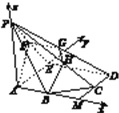
则A(0,0,0)，B(1,0,0)，C(2,1,0)，P(0,0,2)，F(0,1,1)，＝(1,1,0)．

设平面ABF的法向量为n＝(x，y，z)，则

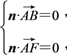即

令z＝1，则y＝－1.所以n＝(0，－1,1)．

设直线BC与平面ABF所成角为α，则

sinα＝|cos<n， >|＝||＝.

因此直线BC与平面ABF所成角的大小为.

设点H的坐标为(u，v，w)．

因为点H在棱PC上，所以可设＝λ (0＜λ＜1)，

即(u，v，w－2)＝λ(2,1，－2)，

所以u＝2λ，u＝λ，w＝2－2λ.

因为n是平面ABF的法向量，所以n·＝0，

即(0，－1,1)·(2λ，λ，2－2λ)＝0.

解得λ＝，所以点H的坐标为(，，)．

所以PH＝＝2.