题目内容
【题目】我国是世界上严重缺水的国家.某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨).将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)估计居民月均水量的中位数.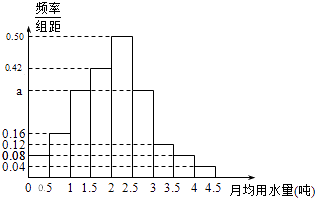
【答案】解:(I)∵1=(0.08+0.16+a+0.40+0.52+a+0.12+0.08+0.04)×0.5,
整理可得:2=1.4+2a,
∴解得:a=0.3.
(II)估计全市居民中月均用水量不低于3吨的人数为3.6万,理由如下:
由已知中的频率分布直方图可得月均用水量不低于3吨的频率为(0.12+0.08+0.04)×0.5=0.12,
又样本容量为30万,
则样本中月均用水量不低于3吨的户数为30×0.12=3.6万.
(Ⅲ)根据频率分布直方图,得;
0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5=0.48<0.5,
0.48+0.5×0.52=0.74>0.5,
∴中位数应在(2,2.5]组内,设出未知数x,
令0.08×0.5+0.16×0.5+0.30×0.5+0.42×0.5+0.52×x=0.5,
解得x=0.04;
∴中位数是2+0.04=2.04.
【解析】(I)先根据频率分布直方图中的频率等于纵坐标乘以组距求出9个矩形的面积即频率,再根据直方图的总频率为1求出a的值;(II)根据已知中的频率分布直方图先求出月均用水量不低于3吨的频率,结合样本容量为30万,进而得解.(Ⅲ)根据频率分布直方图,求出使直方图中左右两边频率相等对应的横坐标的值.
【考点精析】根据题目的已知条件,利用频率分布直方图和平均数、中位数、众数的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据.