题目内容
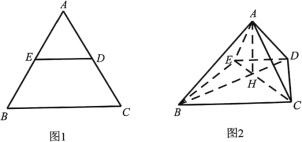
【题目】如图1,在边长为2的等边![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,将AED沿
的中点,将AED沿![]() 折起,使得
折起,使得![]() ,
, ![]() ,得到如图2的四棱锥A-BCDE,连结
,得到如图2的四棱锥A-BCDE,连结![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由题意可得![]() ,
,![]() ,即可得
,即可得![]() ,
, ![]() ,利用线面垂直的判定即可得证;
,利用线面垂直的判定即可得证;
(2)建立空间直角坐标系后,表示出各点坐标,求出平面![]() 、平面
、平面![]() 的一个法向量为
的一个法向量为![]() 、
、![]() ,利用
,利用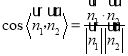 即可得解.
即可得解.
(1)证明:由题意![]() ,
,![]() ,
,
因为![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
所以![]() 且相似比为2,所以
且相似比为2,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
又因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
由![]() 可得
可得![]() 平面
平面![]() ,得证.
,得证.
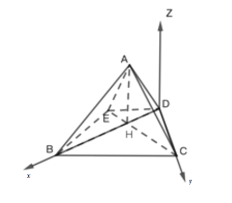
(2)如图,过D作![]() 平面
平面![]() ,DB为x轴,DC为y轴,Dz为z轴,建立空间直角坐标系;
,DB为x轴,DC为y轴,Dz为z轴,建立空间直角坐标系;
所以![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() ,则
,则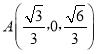 ,
,
由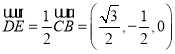 可知
可知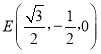 ,
,
所以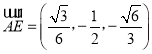 ,
,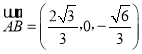 ,
,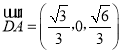 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以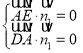 ,即
,即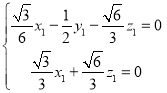 ,取
,取![]() 得
得![]() ,
,
同理可得平面![]() 的一个法向量
的一个法向量![]() ,
,
所以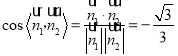 ,
,
由图可知,所求二面角为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如下列联表:
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3:8.
![]() 分别求样本中城市人中的不买房人数和农村人中的纠结人数;
分别求样本中城市人中的不买房人数和农村人中的纠结人数;
![]() 用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
参考公式:![]() .
.
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|