题目内容
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
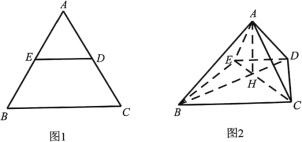
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.


【答案】![]()
![]()
【解析】
(1)以AB为![]() 轴,AD为
轴,AD为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的坐标系,设
轴,建立如图所示的坐标系,设![]() ,求出点P的轨迹为
,求出点P的轨迹为![]() ,即得解;(2)先求出点P的轨迹为
,即得解;(2)先求出点P的轨迹为![]() ,P到平面
,P到平面![]() 的距离为
的距离为![]() ,再求出
,再求出![]() 的最小值即得解.
的最小值即得解.

(1)以AB为![]() 轴,AD为
轴,AD为![]() 轴,
轴,![]() 为
为![]() 轴,建立如图所示的坐标系,则
轴,建立如图所示的坐标系,则![]() 设
设![]() ,
,
由![]() 得
得![]() ,
,
所以![]() ,
,
所以若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为
所形成的阿氏圆的半径为![]() .
.
(2)设点![]() ,由
,由![]() 得
得![]() ,
,
所以![]() ,
,
由题得![]()
所以![]() 设平面
设平面![]() 的法向量为
的法向量为![]() ,
,
所以 ,
,
由题得![]() ,
,
所以点P到平面![]() 的距离为
的距离为 ,
,
因为![]() ,
,
所以![]() ,所以点M到平面
,所以点M到平面![]() 的最小距离为
的最小距离为![]() ,
,
由题得![]() 为等边三角形,且边长为
为等边三角形,且边长为![]() ,
,
所以三棱锥![]() 的体积的最小值为
的体积的最小值为![]() .
.
故答案为:(1). ![]() (2).
(2). ![]() .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.
调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列表,并判断是否由
列表,并判断是否由![]() 的把握认为.了解阿基米德与选择文理科有关?
的把握认为.了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | p> | ||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取两人,求两人都是文科生的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.