题目内容
已知c>0，设命题p：函数y＝cx为减函数．命题q：当x∈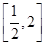
时，函数f(x)＝x＋
>
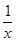恒成立．如果p或q为真命题，p且q为假命题，求c的取值范围．
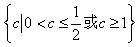
解析
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
补充习题江苏系列答案学练快车道口算心算速算天天练系列答案题目内容
已知c>0，设命题p：函数y＝cx为减函数．命题q：当x∈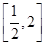时，函数f(x)＝x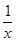＋>恒成立．如果p或q为真命题，p且q为假命题，求c的取值范围．
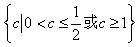
解析
补充习题江苏系列答案学练快车道口算心算速算天天练系列答案
：函数y=1+log
(2x+3)的图像恒过点（-1, 1）；命题
：函数
=2sin|x|+1的图像关于y轴对称. 则下列命题: 
, 
, 
,
,
中真命题个数是_________
,命题乙为：
,则甲是乙的 条件
；
,若
是
的必要非充分条件，求实数
的取值范围．
：方程
有两个不等的负实根，命题
：方程
无实根。若
为真，
的取值范围．
，设p：函数
在(0，＋∞)上单调递减，
”的否定是“
”；
的不等式
恒成立，则
的取值范围是
；
，则有当
时，
，使得函数 
在
上有三个零点；
，且
是常数，又
的最小值是
，则
7.其中正确的个数是 .