题目内容
【题目】已知函数![]() ,且
,且![]() ,则
,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意,由函数的解析式求出函数的定义域,设g(x)=f(x)﹣1,分析可得g(x)为奇函数且在(﹣1,1)上为增函数,据此f(a)+f(a+1)>2 ,解可得a的取值范围,即可得答案.
,解可得a的取值范围,即可得答案.
根据题意,函数f(x)=ln![]() x+1,有
x+1,有![]() 0,解可得﹣1<x<1,即函数f(x)的定义域为(﹣1,1),
0,解可得﹣1<x<1,即函数f(x)的定义域为(﹣1,1),
设g(x)=f(x)﹣1=ln![]() x,则g(﹣x)=ln
x,则g(﹣x)=ln![]() (﹣x)=﹣[ln
(﹣x)=﹣[ln![]() x]=﹣g(x),则函数g(x)为奇函数;
x]=﹣g(x),则函数g(x)为奇函数;
分析易得:g(x)=ln![]() x在(﹣1,1)上为增函数,
x在(﹣1,1)上为增函数,
f(a)+f(a+1)>2f(a)﹣1>﹣[f(a+1)﹣1]g(a)>﹣g(a+1)g(a)>g(﹣a﹣1)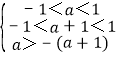 ,
,
解可得:![]() a<0,即a的取值范围为(
a<0,即a的取值范围为(![]() ,0);
,0);
故选:C.

【题目】设相互垂直的直线![]() ,
,![]() 分别过椭圆
分别过椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,且与椭圆
,且与椭圆![]() 的交点分别为
的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() .
.
(1)当![]() 的倾斜角为
的倾斜角为![]() 时,求以
时,求以![]() 为直径的圆的标准方程;
为直径的圆的标准方程;
(2)问是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【题目】“工资条里显红利,个税新政人民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.
新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税级数 | 每月应纳税所得额(含税)=收入-个税起征点 | 税率(%) | 每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除 | 税率(%) |
1 | 不超过1500元部分 | 3 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元部分 | 10 | 超过3000元至12000元部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元部分 | 30 | 超过35000元至55000元部分 | 30 |
··· | ··· | ··· | ··· | ··· |
随机抽取某市1000名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)设该市该收入层级的![]() 从业者2019年月缴个税为
从业者2019年月缴个税为![]() 元,求
元,求![]() 的分布列和期望;
的分布列和期望;
(2)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴交的个税之和就超过2019年的月收入?
从业者各月少缴交的个税之和就超过2019年的月收入?