题目内容
已知a、b是不全为0的实数,求证:方程3ax2+2bx-(a+b)=0在(0,1)内一定有实根.
证明见解析
证明 若a=0时,则b≠0,
此时方程的根为x=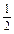 ,满足题意.
,满足题意.
当a≠0时,令f(x)=3ax2+2bx-(a+b).
(1)若a(a+b)<0,
则f(0)·f(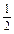 )=-(a+b)·(-
)=-(a+b)·(-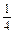 a)=
a)=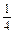 a(a+b)<0,
a(a+b)<0,
所以f(x)在区间(0,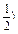 内有一实根.
内有一实根.
(2)若a(a+b)≥0,
则f(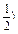 f(1)=(-
f(1)=(-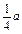 )(2a+b)
)(2a+b)
=-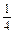 a2-
a2-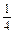 a(a+b)<0,
a(a+b)<0,
所以f(x)在区间(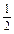 ,1)内有一实根.
,1)内有一实根.
综上所述,方程3ax2+2bx-(a+b)=0在(0,1)内一定有实根.
此时方程的根为x=
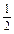 ,满足题意.
,满足题意.当a≠0时,令f(x)=3ax2+2bx-(a+b).
(1)若a(a+b)<0,
则f(0)·f(
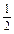 )=-(a+b)·(-
)=-(a+b)·(-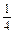 a)=
a)=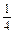 a(a+b)<0,
a(a+b)<0,所以f(x)在区间(0,
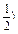 内有一实根.
内有一实根.(2)若a(a+b)≥0,
则f(
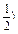 f(1)=(-
f(1)=(-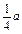 )(2a+b)
)(2a+b)=-
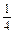 a2-
a2-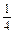 a(a+b)<0,
a(a+b)<0,所以f(x)在区间(
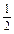 ,1)内有一实根.
,1)内有一实根.综上所述,方程3ax2+2bx-(a+b)=0在(0,1)内一定有实根.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
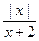
 -3.
-3.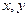 满足:
满足: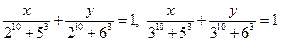 ,则
,则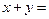 .
.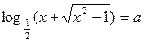 有解,则实数a的取值范围是_________________
有解,则实数a的取值范围是_________________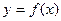 的图象在
的图象在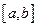 上连续,若满足 ,方程
上连续,若满足 ,方程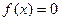

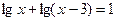 的解为( )
的解为( ) 或
或
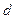 的的值。
的的值。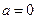 ,求
,求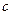 的取值范围;
的取值范围;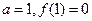 ,求
,求