题目内容
【题目】某玩具厂生产出一种新型儿童泡沫玩具飞机,为更精确的确定最终售价,该厂采用了多种价格对该玩具飞机进行了试销,某销售点的销售情况如下表:
单价 | 8 | 9 | 10 | 11 | 12 |
销量 | 40 | 36 | 30 | 24 | 20 |
从散点图可以看出,这些点大致分布在一条直线的附近,变量![]() ,
,![]() 有较强的线性相关性.
有较强的线性相关性.
(1)求销量![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若每架该玩具飞机的成本价为5元,利用(1)的结果,预测每架该玩具飞机的定价为多少元时,总利润最大.(结果保留一位小数)
(附: ,
,![]() ,
,![]() ,
,![]() .)
.)
【答案】(1)![]() ;(2)10.4元.
;(2)10.4元.
【解析】
(1)由参考数据,结合表格,分别求得![]() 与
与![]() 即可求得回归直线方程;
即可求得回归直线方程;
(2)由(1)中回归直线方程,可得销量,从而利用销量![]() 单件利润,计算总利润.
单件利润,计算总利润.
(1)由表中数据得![]() ,
,![]() ,故:
,故:
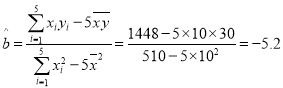 ,
,
![]() .
.
所以回归方程为![]() .
.
(2)设定价为![]() 元时,总利润为
元时,总利润为![]() 元,
元,
则![]() ,
,
所以![]() 时,
时,![]() 取最大值.
取最大值.
即当定价为10.4元时,总利润最大.

练习册系列答案
相关题目
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.