题目内容
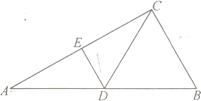
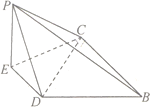
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中点,
的中点,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影为点
上的正投影为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
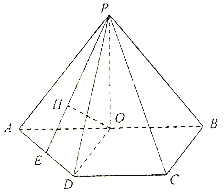
(1)求证:![]() 为
为![]() 中点;
中点;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)连接OE,可得四边形BCDO是平行四边形,由PO⊥底面ABCD.O在平面PAD上的正投影为点H,可得AD⊥OE,又AO=OD,即可得E为AD中点;(2)以O为原点建立空间直角坐标系,设![]() ,∴
,∴![]() ,∴
,∴![]() ,又
,又![]() 是平面PAB的法向量,求出面PCD的法向量,即可求得OG与面PCD所成角的正弦值.
是平面PAB的法向量,求出面PCD的法向量,即可求得OG与面PCD所成角的正弦值.
详解:(1)连结![]() ,∵
,∵![]() ,
,![]() 是
是![]() 中点,
中点,![]() ,
,

∴![]() ,∵
,∵![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() 在平面
在平面![]() 的正投影为
的正投影为![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 是
是![]() 的中点.
的中点.
(2)∵![]() ,
,![]() ,∴
,∴![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的正方向建立空间直角坐标系
的正方向建立空间直角坐标系![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() 是
是![]() 的外心,∵
的外心,∵![]() ,
,
∴![]() 是
是![]() 的重心,∴
的重心,∴![]() ,
,
设![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() 是平面
是平面![]() 的一个法向量,且
的一个法向量,且![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
设![]() 是平面
是平面![]() 的法向量,∵
的法向量,∵![]() ,
,![]() ,
,
∴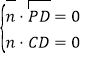 ,即
,即![]() ,取
,取![]() ,则
,则![]() ,
,![]() ,∴
,∴![]()
∴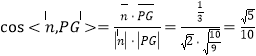 ,∴直线
,∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】某玩具厂生产出一种新型儿童泡沫玩具飞机,为更精确的确定最终售价,该厂采用了多种价格对该玩具飞机进行了试销,某销售点的销售情况如下表:
单价 | 8 | 9 | 10 | 11 | 12 |
销量 | 40 | 36 | 30 | 24 | 20 |
从散点图可以看出,这些点大致分布在一条直线的附近,变量![]() ,
,![]() 有较强的线性相关性.
有较强的线性相关性.
(1)求销量![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若每架该玩具飞机的成本价为5元,利用(1)的结果,预测每架该玩具飞机的定价为多少元时,总利润最大.(结果保留一位小数)
(附: ,
,![]() ,
,![]() ,
,![]() .)
.)
【题目】某客户准备在家中安装一套净水系统,该系统为三级过滤,使用寿命为十年.如图所示,两个一级过滤器采用并联安装,二级过滤器与三级过滤器为串联安装。

其中每一级过滤都由核心部件滤芯来实现。在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立),三级滤芯无需更换,若客户在安装净水系统的同时购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.若客户在使用过程中单独购买滤芯,则一级滤芯每个
元.若客户在使用过程中单独购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据
元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据![]() 套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据
套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据![]() 个一级过滤器更换的滤芯个数制成的柱状图,表是根据
个一级过滤器更换的滤芯个数制成的柱状图,表是根据![]() 个二级过滤器更换的滤芯个数制成的频数分布表.
个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表
二级滤芯更换的个数 |
|
|
频数 |
|
|
以![]() 个一级过滤器更换滤芯的频率代替
个一级过滤器更换滤芯的频率代替![]() 个一级过滤器更换滤芯发生的概率,以
个一级过滤器更换滤芯发生的概率,以![]() 个二级过滤器更换滤芯的频率代替
个二级过滤器更换滤芯的频率代替![]() 个二级过滤器更换滤芯发生的概率.
个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为![]() 的概率;
的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() ,
,![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() ,
,![]() 的值.
的值.