Question

【题目】为了了解居民的家庭收人情况,某社区组织工作人员从该社区的居民中随机抽取了户家庭进行问卷调查.经调查发现,这些家庭的月收人在元到元之间，根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一 、二、四小组的频率之比为,且第四小组的频数为.

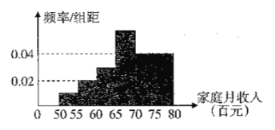
(1)求;

(2)求这户家庭月收人的众数与中位数(结果精确到);

(3)这户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取户家庭,并从这户家庭中随机抽取户家庭进行慰问,求这户家庭月收入都不超过元的概率.

Answer 1

【答案】（1） （2）众数是67.5，中位数是66.3 （3）

【解析】

（1）根据从左至右第一 、二、四小组的频率之比为,求出第四小组的频率，再由频率即可求解.

（2）由频率分布直方图第四组小矩形底边中点的横坐标为众数；中位数等于各个小矩形面积与其小矩形底边中点横坐标之积的和.

（3）根据分层抽样得出第一、二、三小组应分别抽取，分别记记为

依次列出基本事件个数，由古典概型的概率求法公式即可求解.

解：（Ⅰ）设从左至右第一、三、四小组的频率分别为，则由题意可知：

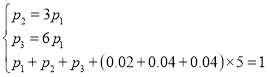,解得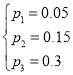

从而

（2）由于第四小组频率最大，故这 户家庭月收入的众数为

由于前四小组的频率之和为：

故这户家庭月收入的中位数应落在第四小组，设中位数为

则，解得

（3）因为家庭月收入在第一、二、三小组的家庭分别有户，按照分层抽样的方法易知分别抽取，第一组记为，第二组，第三组为，

从中随机抽取2 户家庭的方法共有共种；

其中这户家庭月收入都不超过元的有

共种；

所以这户家庭月收入都不超过元的概率为