题目内容
(本小题满分12分)
已知函数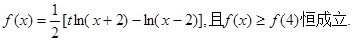
(I)求x为何值时,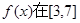 上取得最大值;
上取得最大值;
(II)设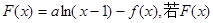 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.
已知函数
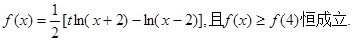
(I)求x为何值时,
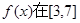 上取得最大值;
上取得最大值;(II)设
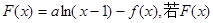 是单调递增函数,求a的取值范围.
是单调递增函数,求a的取值范围.(I)7;(II)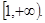 。
。
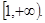 。
。试题分析:(I)
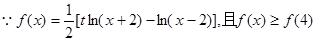 恒成立,
恒成立,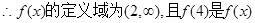 的最小值
的最小值又
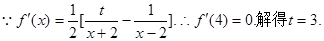 ……………………3分
……………………3分∴
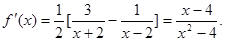
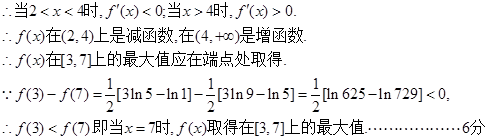
(II)∵ F(x)是单调递增函数,
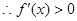 恒成立
恒成立又
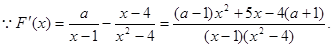
显然在
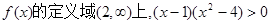 恒成立.
恒成立.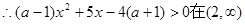 恒成立. ………………………………8分
恒成立. ………………………………8分下面分情况讨论
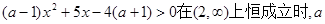 的解的情况.
的解的情况.当
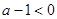 时,显然不可能有
时,显然不可能有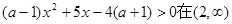 上恒成立.
上恒成立.当
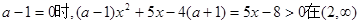 上恒成立.
上恒成立.当
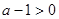 时,又有两种情况:①
时,又有两种情况:①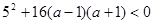 ;
;②
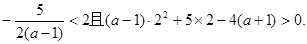 由①得
由①得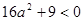 ,无解;由②得
,无解;由②得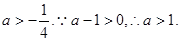
综上所述各种情况,当
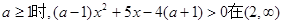 上恒成立.
上恒成立.∴所求的a的取值范围为
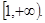 ……………12分
……………12分点评:本题主要考查导数的基本性质和应用、对数函数性质和平均值不等式等知识以及综合推理论证的能力,考查函数的单调性与其导函数的正负之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
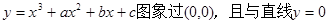 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为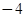 ;
;
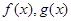 是定义在R上可导函数,满足
是定义在R上可导函数,满足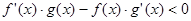 ,且
,且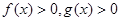 ,对
,对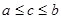 时。下列式子正确的是( )
时。下列式子正确的是( )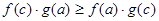
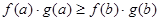
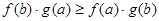

 中,若
中,若 ,则
,则 的值是
的值是  (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份, )的函数解析式.
)的函数解析式. 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求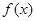 的定义域为D,若对任意的
的定义域为D,若对任意的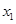 、
、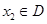 ,当
,当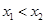 时,都有
时,都有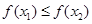 ,则称函数
,则称函数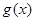 在
在 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1)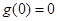 ;(2)
;(2)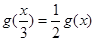 ;(3)
;(3)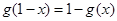 ,则
,则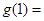 、
、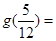 .
.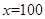 与函数
与函数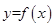 的图象的交点个数是 ( )
的图象的交点个数是 ( )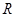 上的函数
上的函数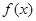 满足以下条件:
满足以下条件: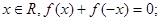 (2)对任意
(2)对任意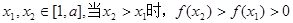 .
.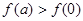 ;②
;②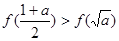 ;③
;③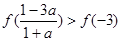 ;④
;④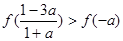 .其中一定成立的是 (请写出所有正确的序号)
.其中一定成立的是 (请写出所有正确的序号)