题目内容
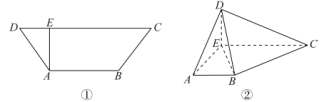
【题目】如图,在多面体![]() 中,
中,![]() 为矩形,
为矩形,![]() 为等腰梯形,
为等腰梯形,![]() ,
,![]() ,
,![]() ,且
,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
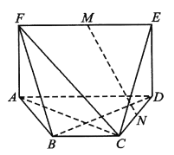
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求多面体
,求多面体![]() 的体积.
的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() .连接
.连接![]() ,
,![]() ,先证明平面
,先证明平面![]() 平面
平面![]() ,然后可证明结论.
,然后可证明结论.
(Ⅱ)过![]() 作
作![]() ,垂直为
,垂直为![]() ,连接
,连接![]() ,可得
,可得![]() 面平面
面平面![]() ,可得
,可得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,在直角
所成的角,在直角![]() 中,由射影定理可得
中,由射影定理可得![]() ,由
,由![]() ,则
,则![]() ,可求得
,可求得![]() ,从而求得
,从而求得![]() ,再根据
,再根据![]() 可求得体积.
可求得体积.
解:(Ⅰ)如图,取![]() 的中点
的中点![]() .连接
.连接![]() ,
,![]() .
.
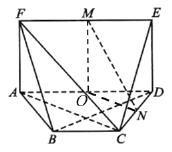
在矩形![]() 中,∵
中,∵![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,
的中点,
∴![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,
的中点,
∴![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)如图,过![]() 作
作![]() ,垂直为
,垂直为![]() ,连接
,连接![]() .
.
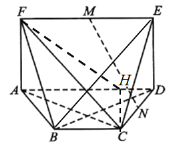
面平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 面平面
面平面![]() ,则
,则![]() 为
为![]() 在平面
在平面![]() 上的射影.
上的射影.
所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角
所成的角
则![]() ,则
,则![]()
在等腰梯形![]() 中,
中,![]() ,
,![]() ,则
,则![]()
由![]() ,则有
,则有![]() ,
,
在直角![]() 中,由射影定理有,
中,由射影定理有,![]() ,则
,则![]()
在直角![]() 中,
中,![]() ,得
,得![]()
又在直角![]() 中,
中, ![]() ,得
,得![]() ,所以
,所以![]()
连接![]() .
.
∴![]()
![]()
![]() .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: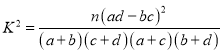 .
.
|
|
|
|
|
|
|
|
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式
满足关系式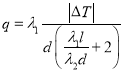 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米·度),不流通、干燥空气的热传导系数
焦耳/(厘米·度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 为室内外温度差,
为室内外温度差,![]() 值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 | 玻璃间夹空气层厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
则保温效果最好的双层玻璃的型号是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型