若5=a0+a1x+a2x2+a3x3+a4x4+a5x5.则a1+2a2+3a3+4a4+5a5等于( )A．5B．25C．-5D．-25 题目和参考答案——青夏教育精英家教网——

题目内容

15．若（5x-4）⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵，则a₁+2a₂+3a₃+4a₄+5a₅等于（　　）

A．

5

B．

25

C．

-5

D．

-25

分析把所给的等式两边对x求导，可得 25（5x-4）⁴=a₁+2a₂x+3a₃x²+4a₄x³+5a₅x⁴，再令x=1，可得 a₁+2a₂+3a₃+4a₄+5a₅ 的值．

解答解：对于（5x-4）⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵，两边对x求导，
可得 25（5x-4）⁴=a₁+2a₂x+3a₃x²+4a₄x³+5a₅x⁴，
再令x=1，可得 a₁+2a₂+3a₃+4a₄+5a₅=25，
故选：B．

点评本题主要考查求函数的导数，二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基础题．

练习册系列答案

百分学生作业本题练王系列答案

小学1课3练培优作业本系列答案

中华题王系列答案

优翼学练优系列答案

优加学习方案系列答案

52045模块式全能训练系列答案

钟书金牌新教材全练系列答案

4560课时双测系列答案

百所名校精点试题系列答案

互动课堂系列答案

相关题目

5．已知函数f（x）=alnx-2x，g（x）=x²-（2-a）x-（2-a）lnx，其中a∈R．
（1）判断f（x）单调性；
（2）若g（x）在其定义域内为增函数，求正实数a的取值范围；
（3）若F（x）=f（x）-g（x）函数存在两个零点m、n，且2x₀=m+n，问：函数F（x）在点（x₀，F（x₀））处的切线能否平行于x轴？

6．某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为研究工人的日平均生产量是否与年龄有关．现采用分层抽样的方法，从中抽取了100名工人作为样本，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，在将两组工人的日平均生产件数分成5组：[50，60），[60，70），[70，80），[80，90），[90，100）分别加以统计，得到如图所示的频率分布直方图．
（1）从样本100人中抽取日平均生产件数[60，70）的工人，求“25周岁以上组”和“25周岁以下组”工人的各抽取多少人？
（2）规定日平均生产件数不少于80件者为“生产能手”，请你根据已知条件完成2×2的列联表，并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”？
附：x²=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$

P（x²≥k）	0.100	0.050	0.010	0.001
k	2.706	3.841	6.635	10.828

3．（1）设a＞b＞0，试比较$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}$与$\frac{a-b}{a+b}$的大小．
（2）设不等式x²-4x+3＜0的解集为A，不等式x²+x-6＞0的解集为B．若不等式x²+ax+b＜0的解集为A∩B，求a，b的值．

10．已知函数f（x）=$\frac{e^x}{x+a}$，（a＜3且a∈Z），且函数f（x）在区间（-1，0）上单调递增，定义在R上的函数g（x）=（x+b）（x²-8），且函数g（x）在x=1处的切线与直线x-y=0垂直．
（Ⅰ）求函数f（x）与函数g（x）的解析式；
（Ⅱ）已知函数F（x）=$\left\{\begin{array}{l}f（x）•g（x），x≠-2\\-4{e^{-2}}，x=-2\end{array}$，试问：是否存在实数a，b，其中[a，b]⊆（-∞，4]，使得函数F（x）的值域也为[a，b]？若能，请求出相应的a、b；若不能，请说明理由．

李克强总理4月22日（世界读书日前一天）在厦门大学考察时，指出世界读书日虽然只有一天，但我们应该天天读书，这种好习惯会让我们终身受益．
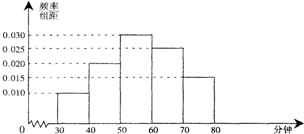
某中学在此期间开展了一系列的读书教育活动．为了解本校学生课外阅读情况，学校随机抽取了100名学生进行调查．右侧是根据调查结果绘制的学生日均课外阅读时间（单位：分钟）的频率分布直方图．若将日均阅读时间
不低于60分钟的学生称为“读书迷”，低于60分钟的学生称为“非读书迷”．
（Ⅰ）根据已知条件完成下面2×2的列联表，并据此判断是否有99%的把握认为“读书迷”与性别有关？

	非读书迷	读书迷	总计
男		15
女			45
总计

P（K²≥k₁）	0.100	0.050	0.010	0.001
k₁	2.706	3.841	6.635	10.828

（Ⅱ）将频率视为概率，现从该校大量学生中用随机抽样的方法每次抽取1人，共抽取5次，记被抽取的5人中的“读书迷”的人数为X．若每次抽取的结果是相互独立的，求X的数学期望EX和方差DX．
附：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

7．已知函数f（x）=$\sqrt{3}$sinxcosx-cos²x+1
（1）求函数f（x）的单调递增区间；
（2）若f（$\frac{θ}{2}$+$\frac{π}{12}$）=$\frac{5}{6}$，θ∈（0，$\frac{π}{2}$），求cos（θ+$\frac{π}{4}$）的值．

4．已知函数f（x）的定义域为[0，1]，求下列函数的定义域：
（1）f（x²）；
（2）f（$\sqrt{x}$-1）

5．某校卫生所成立了调查小组，调查“按时刷牙与患龋齿的关系”，对该校某年级700 名学生进行检查，按患龋齿和不患龋齿分类，得汇总数据：按时刷牙且不患龋齿的学生有60 名，不按时刷牙但不患龋齿的学生有100 名，按时刷牙但患龋齿的学生有 140 名．
（1）能否在犯错概率不超过 0.01 的前提下，认为该年级学生的按时刷牙与患龋齿有关系？
（2）4名校卫生所工作人员甲、乙、丙、丁被随机分成两组，每组 2 人，一组负责数据收集，
另一组负责数据处理，求工作人员甲分到“负责收集数据组”并且工作人员乙分到“负责数据处理组”的概率

P（K²≥k₀）	0.010	0.005	0.001
k₀	6.635	7.879	10.828

附：k²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．