题目内容
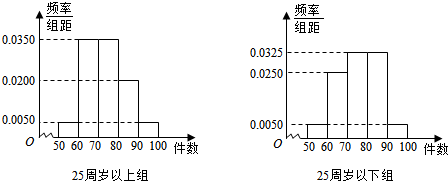
6.某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人作为样本,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图所示的频率分布直方图.(1)从样本100人中抽取日平均生产件数[60,70)的工人,求“25周岁以上组”和“25周岁以下组”工人的各抽取多少人?
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成2×2的列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
附:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$
| P(x2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
分析 (1)根据分层抽样原理,结合频率分布直方图,求出每组应抽取的人数;
(2)由频率分布直方图,计算各组对应的生产能手数,填写2×2列联表,计算K2的值,从而得出统计结论.
解答 解:(1)根据分层抽样原理,得;
样本中有25周岁以上组工人60名,25周岁以下组工人40名,
所以,“25周岁以上组”应抽取60×0.035×10=21人,
“25周岁以下组”应抽取40×0.025×10=10人;
(2)由频率分布直方图知,在抽取的100名工人中,
“25周岁以上组”中的生产能手60×0.25=15(人),
“25周岁以下组”中的生产能手40×0.375=15(人),
据此可得2×2列联表如下:
| 生产能手 | 非生产能手 | 合计 | |
| 25周岁以上组 | 15 | 45 | 60 |
| 25周岁以下组 | 15 | 25 | 40 |
| 合计 | 30 | 70 | 100 |
因为1.79<2.706,所以没有90%的把握认为“生产能手与工人所在的年龄组有关”.
点评 本题考查了频率分布直方图的应用问题,也考查了分层抽样方法的应用问题,考查了2×2列联表的应用问题,是基础题目.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
16.某中学共2200名学生中有男生1200名,按男女性别用分层抽样的方法抽出110名学生,询问是否爱好某项运动.已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动.
(1)完成如下的列联表:
(2)通过计算说明,是否在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别有关”?
(1)完成如下的列联表:
| 男 | 女 | 总计 | |
| 爱好 | 40 | ||
| 不爱好 | 30 | ||
| 总计 |
1.已知随机变量X~N(0,1),则X在区间(-3,+∞)内概率为( )
| A. | 0.8874 | B. | 0.0026 | C. | 0.0013 | D. | 0.9987 |
15.若(5x-4)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a1+2a2+3a3+4a4+5a5等于( )
| A. | 5 | B. | 25 | C. | -5 | D. | -25 |