题目内容
19.已知圆C:(x-1)2+(y-4)2=r2(r>0)(Ⅰ)若直线x-y+5=0与圆C相交所得弦长为$2\sqrt{2}$,求半径r;
(Ⅱ)已知原点O,点A(2,0),若圆C上存在点P,使得$|PO|=\sqrt{2}|PA|$,求半径r的取值范围.
分析 (Ⅰ)求出C到直线x-y+5=0的距离,根据直线x-y+5=0与圆C相交所得弦长为$2\sqrt{2}$,利用勾股定理,即可求半径r;
(Ⅱ)由$|PO|=\sqrt{2}|PA|$可得(x-4)2+y2=8,所以只需要圆C和圆(x-4)2+y2=8有公共点.
解答 解:(Ⅰ)C到直线x-y+5=0的距离为d=$\frac{|1-4+5|}{\sqrt{2}}$=$\sqrt{2}$,直线与圆相交所得弦长为$2\sqrt{2}$,所以$r=\sqrt{2+2}=2$.
(Ⅱ)设P(x,y),由$|PO|=\sqrt{2}|PA|$可得(x-4)2+y2=8,
所以只需要圆C和圆(x-4)2+y2=8有公共点,两圆圆心距离为5,
所以$5-2\sqrt{2}≤r≤5+2\sqrt{2}$.
点评 本题考查直线与圆、圆与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
9.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有( )
| A. | ∠ADE=20° | B. | ∠ADE=30° | C. | ∠ADE=$\frac{1}{3}$∠ADC | D. | ∠ADE=$\frac{1}{2}$∠ADC |
7.设全集U=R,集合$A=\{x|\frac{x-1}{x-2}≥0\}$,则∁UA等于( )
| A. | [1,2] | B. | [1,2) | C. | (1,2] | D. | (1,2) |
14.命题p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6相交.则?p及?p的真假为( )
| A. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为真 | |
| B. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为假 | |
| C. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为真 | |
| D. | ¬p:?a∈R,直线ax+y-2a-1=0与圆x2+y2=6不相交,¬p为假 |
4.若函数y=f(x)为偶函数,且在(0,+∞)上是减函数,又f(3)=0,则$\frac{f(x)+f(-x)}{2x}<0$的解集为( )
| A. | (-3,3) | B. | (-3,0)∪(3,+∞) | C. | (-∞,-3)∪(0,3) | D. | (-∞,-3)∪(3,+∞) |
8.已知等差数列{an}中,a7+a9=16,a4=4,则a6的值是( )
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
9.已知函数$f(x)=\frac{2x+1}{x-1}$,函数g(x)的图象与y=f-1(x)的图象关于y=x对称,则g(-1)的值是( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | 0 | D. | -3 |
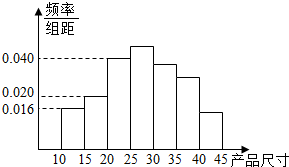 从一条生产线上每隔30分钟取一件产品,共取了n件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在[15,45)内的频数为92.
从一条生产线上每隔30分钟取一件产品,共取了n件,测得其产品尺寸后,画出其频率分布直方图如图,已知尺寸在[15,45)内的频数为92. 若三棱锥的三视图如图,则其表面积为30+6$\sqrt{5}$.
若三棱锥的三视图如图,则其表面积为30+6$\sqrt{5}$.