题目内容
【题目】已知函数
（
，
为实数，
，
）
（1）若函数
的图象过点
，且方程
有且只有一个实根，求的表达式；
（2）在（1）的条件下，当
时，
是单调函数，求实数
的取值范围.
【答案】（1）f(x)= x2+2x+1（2）(-∞,0
∪ [6，+∞）
【解析】试题分析：
(1)由题意得到 关于a,b的方程组，求解方程组，待定系数法可得
的表达式是f(x)=x2+2x+1
(2)利用二次函数的性质 结合函数的对称轴求解不等式 可得实数
的取值范围是(-∞,0∪ [6，+∞）.
试题解析：
(1)f(-2)=1得b=2a 且△=b2-4a=0 所以a=1,b=2 所以f(x)= x2+2x+1
(2) 因为g(x)= x2+(2-k)x+1 所以
2或
-1 即k6或k0
所以k的取值范围 (-∞,0∪[6，+∞）
练习册系列答案
相关题目
【题目】某中学为了了解全校学生的阅读情况，在全校采用随机抽样的方法抽取了60名学生（其中初中组和高中组各30名）进行问卷调查，并将他们在一个月内去图书馆的次数进行了统计，将每组学生去图书馆的次数分为5组： 
，分别制作了如图所示的频率分布表和频率分布直方图.
分组 | 人数 | 频率 |
| 3 | |
| 9 | |
| 9 | |
| 0.2 | |
| 0.1 |
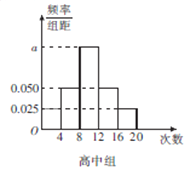
（1）完成频率分布表，并求出频率分布直方图中
的值；
（2）在抽取的60名学生中，从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人，并用
表示抽得的高中组的人数，求
的分布列和数学期望.
