题目内容
【题目】已知函数f(x)=﹣x3+ax2+bx+c图象上的点P(1,m)处的切线方程为y=﹣3x+1
(1)若函数f(x)在x=﹣2时有极值,求f(x)的表达式.
(2)若函数f(x)在区间[﹣2,0]上单调递增,求实数b的取值范围.
【答案】
(1)解:f′(x)=﹣3x2+2ax+b,
∵函数f(x)在x=1处的切线斜率为﹣3,
∴f′(x)=﹣3+2a+b=﹣3,即2a+b=0,
又f(1)=﹣1+a+b+c=﹣2,得a+b+c=﹣1
函数f(x)在x=﹣2时有极值,
∴f′(﹣2)=﹣12﹣4a+b=0,
解得a=﹣2,b=4,c=﹣3,
∴f(x)=﹣x3﹣2x2+4x﹣3
(2)解:∵函数f(x)在区间[﹣2,0]上单调递增,
∴导函数f′(x)=﹣3x2﹣bx+b在区间[﹣2,0]上的值恒大于或等于零,
则 ![]() ,得b≥4,
,得b≥4,
∴实数b的取值范围为[4,+∞).
【解析】(1)求出原函数的导函数,由题意得f′(x)=﹣3,f(1)=﹣2,再结合f′(﹣2)=0联立方程组求得a,b,c的值,则f(x)的表达式可求;(2)把函数f(x)在区间[﹣2,0]上单调递增转化为f′(x)=﹣3x2﹣bx+b在区间[﹣2,0]上的值恒大于或等于零,进一步转化为关于b的不等式组得答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
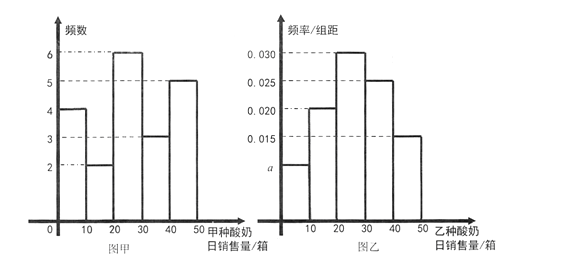
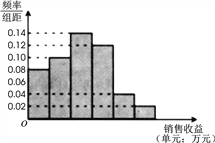
小学生10分钟应用题系列答案【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.
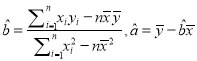
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中 )
)