题目内容
【题目】已知函数![]() .
.
(1)若不等式![]() 的解集为
的解集为![]() ,求不等式
,求不等式![]() 的解集;
的解集;
(2)![]() 时,
时,
①当![]() 时,若不等式
时,若不等式![]() 在
在![]() 有解,求
有解,求![]() 的取值范围;
的取值范围;
②当![]() 时,设
时,设![]() ,若存在
,若存在![]() ,
,![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或
或![]() (2)①
(2)①![]() ,②
,②![]() .
.
【解析】
(1)转化条件得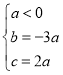 ,不等式可转化为
,不等式可转化为![]() ,解不等式即可得解;
,解不等式即可得解;
(2)①转化条件得![]() 在
在![]() 上有解,求出函数
上有解,求出函数![]() 在
在![]() 时的最大值即可得解;
时的最大值即可得解;
②转化条件得方程![]() 有两个不相等实数根且
有两个不相等实数根且![]() 在
在![]() 时有解,令
时有解,令![]() ,
,![]() ,求出
,求出![]() 的取值范围结合
的取值范围结合![]() 即可得解.
即可得解.
(1)![]() 不等式
不等式![]() 的解集为
的解集为![]() ,
,
![]()
![]() 且
且![]() 即
即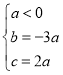 ,
,
![]() 原不等式可转化为
原不等式可转化为![]() 即
即![]() ,
,
解得![]() 或
或![]() .
.
![]() 不等式
不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(2)①由题意得![]() 在
在![]() 上有解即
上有解即![]() 在
在![]() 上有解,
上有解,
令![]() ,则
,则 ,
,
当![]() 时,
时,![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() .
.
②![]()
![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,
成立,
![]() 方程
方程![]() 有两个不相等实数根且在
有两个不相等实数根且在![]() 时有解,
时有解,
![]()
![]() 解得
解得![]() 或
或![]() ;
;
![]()
![]() 在
在![]() 时有解,
时有解,
令![]() ,
,![]() ,则
,则![]() 在
在![]() 时有解,
时有解,
令![]() ,
,![]() ,
,
![]()
![]() 在
在![]() 时单调递减,在
时单调递减,在![]() 时单调递增,
时单调递增,
又 ![]() ,
,![]() ,
,![]() ,
,
![]()
![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
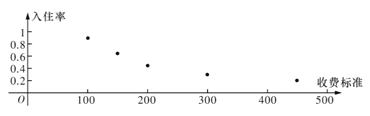
【题目】某创业者计划在某旅游景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向此创业者对该景区附近五家“农家乐”跟踪调查了100天,这五家“农家乐的收费标准互不相同得到的统计数据如下表,x为收费标准(单位:元/日),t为入住天数(单位:天),以频率作为各自的“入住率”,收费标准x与“入住率”y的散点图如图
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
(1)若从以上五家“农家乐”中随机抽取两家深人调查,记![]() 为“入住率超过0.6的农家乐的个数,求
为“入住率超过0.6的农家乐的个数,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,
哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,![]() 的结果精确到0.1)
的结果精确到0.1)
(3)根据第(2)问所求的回归方程,试估计收费标准为多少时,100天销售额L最大?(100天销售额L=100×入住率×收费标准x)
参考数据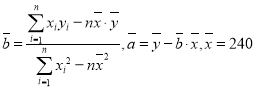 ,
,![]() ,
,![]()
![]()