题目内容

20．设函数f（x）=$\left\{\begin{array}{l}{1-|x-1|，x∈（-∞，2）}\\{\frac{1}{2}f（x-2），x∈[2，+∞）}\end{array}\right.$，则函数F（x）=x•[f（x）+$\frac{3}{10}$]-$\frac{13}{10}$的零点个数为（　　）
A．4B．5C．6D．7

分析 函数F（x）=x•[f（x）+$\frac{3}{10}$]-$\frac{13}{10}$的零点个数可化为方程f（x）=$\frac{13}{10x}$-$\frac{3}{10}$的解的个数，作函数的图象，从而由数形结合求解．

解答 解：令x•[f（x）+$\frac{3}{10}$]-$\frac{13}{10}$=0，
易知x=0不是方程的解，故x≠0；
故f（x）+$\frac{3}{10}$=$\frac{13}{10x}$，
即f（x）=$\frac{13}{10x}$-$\frac{3}{10}$，
作函数y=f（x）与y=$\frac{13}{10x}$-$\frac{3}{10}$的图象如下，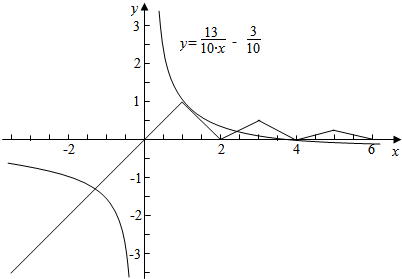
，
结合图象可知，图象有6个交点，
故选：C．

点评 本题考查了数形结合的思想应用及方程的根与函数的零点的关系应用．

练习册系列答案
相关题目
10．给定下列命题：
①“若k＞0，则方程x2+2x-k=0有实数根”的逆否命题；
②“若A=B，则sinA=sinB”的逆命题；
③“若$\frac{1}{a}＜\frac{1}{b}＜0，则\;ab＜b$2”的逆否命题；
④“若xy=0，则x，y中至少有一个为零”的否命题．
⑤“若$\frac{b}{a}＞\frac{a}{b}，则\;a＜b＜0$”的逆命题．
其中真命题的序号是①③④．
11．给出下列四个命题．
①命题p：对任意x∈R，sinx≤1的否定￢p：存在x∈R，sinx＞1；
②“k=1”是“函数y=cos2kx-sin2kx的最小正周期为π”的充要条件；
③若$\overrightarrow{a}$与$\overrightarrow{b}$+$\overrightarrow{c}$都是非零向量，则“$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=$\overrightarrow{0}$”是“$\overrightarrow{a}$∥（$\overrightarrow{b}$+$\overrightarrow{c}$）”的必要不充分条件；
④命题“若一个整数能被6整除，则它能被3整除”的否命题是假命题．其中真命题的序号是①．（写出所有正确命题的序号）．
8．下面四个结论：
①y=sin|x|的图象关于原点对称；
②y=sin（|x|+2）的图象是把y=sin|x|的图象向左平移2个单位而得到的；
③y=sin（x+2）的图象是把y=sinx的图象向左平移2个单位而得到的；
④y=sin（x+2）的图象是由y=sin（x+2）（x≥0）的图象及y=-sin（x-2）（x＜0）的图象组成的．
其中，正确的结论有③（请把正确结论的序号都填上）
15．用导数的定义求函数y=$\sqrt{x}$的导数．
5．在正三棱柱ABC-A1B1C1中，E是AB的中点，D是CC1上一点．
（I）求证：A1B1∥平面DAB；
（Ⅱ）求证：A1B1⊥DE．
12．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）和圆O：x2+y2=b2．过双曲线C上一点P引圆O的两条切线，切点分别为A，B．若△PAB可为正三角形，则双曲线C的离心率e的取值范围是[$\frac{\sqrt{5}}{2}$，+∞）．
9．已知F为抛物线y2=4x的焦点，点A，B在该抛物线上，$\overrightarrow{OA}$$•\overrightarrow{OB}$=0（其中O为坐标原点），则△ABO与△BFO面积之差的最小值是（　　）
A．4B．8C．8$\sqrt{3}$D．16$\sqrt{3}$
10．已知点A（1，2），B（2，3），C（-2，5），证明$\overrightarrow{AB}$⊥$\overrightarrow{AC}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网