题目内容
17.已知平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,点E,F分别在线段BC,DC上运动,设$\overrightarrow{BE}=λ\overrightarrow{BC},\overrightarrow{DF}=\frac{1}{9λ}\overrightarrow{DC}$,则$\overrightarrow{AE}•\overrightarrow{AF}$的最小值是$\frac{22}{9}$.分析 由题意画出图形,把$\overrightarrow{AE},\overrightarrow{AF}$都用含有$\overrightarrow{AB},\overrightarrow{AD}$的式子表示,展开后化为关于λ的函数,再利用基本不等式求最值.
解答  解:如图,
解:如图,
$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BE}=\overrightarrow{AB}+λ\overrightarrow{BC}=\overrightarrow{AB}+λ\overrightarrow{AD}$,
$\overrightarrow{AF}=\overrightarrow{AD}+\overrightarrow{DF}=\overrightarrow{AD}+\frac{1}{9λ}\overrightarrow{DC}=\overrightarrow{AD}+$$\frac{1}{9λ}\overrightarrow{AB}$.
∵AB=2,AD=1,∠DAB=60°,
∴$\overrightarrow{AE}•\overrightarrow{AF}$=$(\overrightarrow{AB}+λ\overrightarrow{AD})•(\overrightarrow{AD}+\frac{1}{9λ}\overrightarrow{AB})$
=$\frac{10}{9}\overrightarrow{AB}•\overrightarrow{AD}+\frac{1}{9λ}$$|\overrightarrow{AB}{|}^{2}+λ|\overrightarrow{AD}{|}^{2}$
=$\frac{4}{9λ}+λ+\frac{10}{9}×2×1×cos60°$
=$\frac{4}{9λ}+λ+\frac{10}{9}$$≥\frac{10}{9}+2\sqrt{\frac{4}{9λ}•λ}=\frac{22}{9}$.
当且仅当$\frac{4}{9λ}=λ$,即$λ=\frac{2}{3}$时,上式等号成立.
故答案为:$\frac{22}{9}$.
点评 本题考查平面向量的数量积运算,考查了向量加法的三角形法则,体现了数学转化思想方法,是中档题.

 阅读快车系列答案
阅读快车系列答案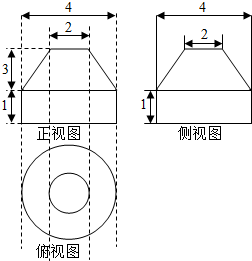 一个几何体的三视图及相关尺寸如图所示,其中其主视图和侧视图是一等腰梯形与一个矩形组成的图形,俯视图是两个同心圆组成的图形,则该几何体的体积为( )
一个几何体的三视图及相关尺寸如图所示,其中其主视图和侧视图是一等腰梯形与一个矩形组成的图形,俯视图是两个同心圆组成的图形,则该几何体的体积为( )| A. | 25π | B. | 19π | C. | 11π | D. | 9π |

| A. | 12π | B. | 24π | C. | 36π | D. | 48π |
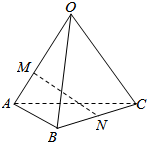 如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )
如图,空间四边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=$\frac{2}{3}$$\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于( )| A. | $\frac{1}{2}\vec a-\frac{2}{3}\vec b+\frac{1}{2}\vec c$ | B. | $-\frac{2}{3}\vec a+\frac{1}{2}\vec b+\frac{1}{2}\vec c$ | C. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b-\frac{1}{2}\vec c$ | D. | $\frac{2}{3}\vec a+\frac{2}{3}\vec b-\frac{1}{2}\vec c$ |