ÌâÄżÄÚÈĘ
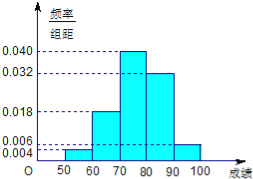
ĄŸÌâÄżĄżÄł°à50ĂûѧÉúÔÚÒ»ŽÎÊęѧČâÊÔÖĐŁŹłÉŒšÈ«ČżœéÓÚ50Óë100ÖźŒäŁŹœ«ČâÊÔœáčû°ŽÈçÏ·œÊœ·ÖłÉÎćŚéŁș”ÚÒ»Śé[50ŁŹ60Ł©ŁŹ”Ú¶țŚé[60ŁŹ70Ł©ŁŹĄŁŹ”ÚÎćŚé[90ŁŹ100].ÈçÍŒËùÊŸÊÇ°ŽÉÏÊö·ÖŚé·œ·š”Ă”œ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒ.
ŁšąńŁ©ÈôłÉŒšŽóÓÚ»ò”ÈÓÚ60ÇÒĐĄÓÚ80ŁŹÈÏÎȘșÏžńŁŹÇóžĂ°àÔÚŐâŽÎÊęѧČâÊÔÖĐłÉŒšșÏžń”ÄÈËÊꣻ
ŁšąòŁ©ŽÓČâÊÔłÉŒšÔÚ[50ŁŹ60Ł©ĄÈ[90ŁŹ100]ÄÚ”ÄËùÓĐѧÉúÖĐËæ»úłéÈĄÁœĂû͏ѧŁŹÉèÆäČâÊÔłÉŒš·Ö±đÎȘmĄąnŁŹÇóÊÂŒțĄ°|m©n|ŁŸ10Ą±žĆÂÊ.
ĄŸŽđ°žĄż
ĄŸœâÎöĄż
ÊÔÌâœâÎöŁșŁšIŁ©ÓÉÖ±·œÍŒÖȘŁŹłÉŒšÔÚ[60ŁŹ80Ł©ÄÚ”ÄÈËÊęÎȘŁș50ĄÁ10ĄÁŁš0.18+0.040Ł©=29.ËùÒԞðàÔÚŐâŽÎÊęѧČâÊÔÖĐłÉŒšșÏžń”ÄÓĐ29ÈË.
ŁšIIŁ©ÓÉÖ±·œÍŒÖȘŁŹłÉŒšÔÚ[50ŁŹ60Ł©ÄÚ”ÄÈËÊęÎȘŁș50ĄÁ10ĄÁ0.004=2ŁŹ
ÉèłÉŒšÎȘxĄąy
łÉŒšÔÚ[90ŁŹ100]”ÄÈËÊęÎȘ50ĄÁ10ĄÁ0.006=3ŁŹÉèłÉŒšÎȘaĄąbĄącŁŹ
ÈômŁŹnĄÊ[50ŁŹ60Ł©Ê±ŁŹÖ»ÓĐxyÒ»ÖÖÇéżöŁŹ
ÈômŁŹnĄÊ[90ŁŹ100]ʱŁŹÓĐabŁŹbcŁŹacÈęÖÖÇéżöŁŹ
ÈômŁŹn·Ö±đÔÚ[50ŁŹ60Ł©șÍ[90ŁŹ100]ÄÚʱŁŹÓĐ
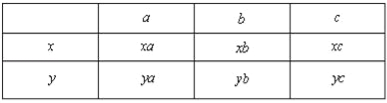
čČÓĐ6ÖÖÇéżöŁŹËùÒÔ»ù±ŸÊÂŒțŚÜÊęÎȘ10ÖÖŁŹ
ÊÂŒțĄ°|m©n|ŁŸ10Ą±Ëù°üșŹ”Ä»ù±ŸÊÂŒțžöÊęÓĐ6ÖÖ
Ąà![]() .
.

 șźŒÙÀÖÔ°±±Ÿ©œÌÓęłö°æÉçÏ”ÁĐŽđ°ž
șźŒÙÀÖÔ°±±Ÿ©œÌÓęłö°æÉçÏ”ÁĐŽđ°ž