题目内容
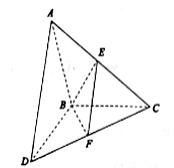
【题目】如图,四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() .
.![]() ,
,![]() .
.
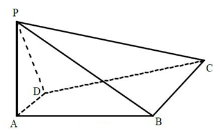
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若平面![]() 内有一经过点
内有一经过点![]() 的曲线
的曲线![]() ,该曲线上的任一动点
,该曲线上的任一动点![]() 都满足
都满足![]() 与
与![]() 所成角的大小恰等于
所成角的大小恰等于![]() 与
与![]() 所成角.试判断曲线
所成角.试判断曲线![]() 的形状并说明理由;
的形状并说明理由;
(3)在平面![]() 内,设点
内,设点![]() 是(2)题中的曲线
是(2)题中的曲线![]() 在直角梯形
在直角梯形![]() 内部(包括边界)的一段曲线
内部(包括边界)的一段曲线![]() 上的动点,其中
上的动点,其中![]() 为曲线
为曲线![]() 和
和![]() 的交点.以
的交点.以![]() 为圆心,
为圆心,![]() 为半径
为半径![]() 的圆分别与梯形的边
的圆分别与梯形的边![]() 、
、![]() 交于
交于![]() 、
、![]() 两点.当
两点.当![]() 点在曲线段
点在曲线段![]() 上运动时,试求圆半径
上运动时,试求圆半径![]() 的范围及
的范围及![]() 的范围.
的范围.
【答案】(1)![]() ;(2)双曲线;(3)
;(2)双曲线;(3)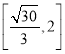 ,
,![]() .
.
【解析】
试题分析:(1)借助题设条件建立空间直角坐标系运用向量的数量积公式求解;(2)在空间坐标系中借助题设建立方程探求;(3)依据题设建立函数关系,运用二次函数的知识及不等式的性质等知识分析探求.
试题解析:
(1)如图,以![]() 为原点,直线
为原点,直线![]() 为
为![]() 轴、直线
轴、直线![]() 为
为![]() 轴、直线
轴、直线![]() 为
为![]() 轴,建立空间直角坐标系.于是有
轴,建立空间直角坐标系.于是有![]() 、
、![]() ,则有
,则有![]() ,又
,又![]()
则异面直线![]() 与
与![]() 所成角
所成角![]() 满足
满足 ,
,
所以,异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
(2)如图,以![]() 为原点,直线
为原点,直线![]() 为
为![]() 轴、直线
轴、直线![]() 为
为![]() 轴、直线
轴、直线![]() 为
为![]() 轴,建立空间直角坐标系.设点
轴,建立空间直角坐标系.设点![]() ,点
,点![]() 、点
、点![]() 、点
、点![]() ,
,
则![]() ,
,![]() ,
,
则![]() ,
,
![]() ,
,
化简整理得到![]() ,
,
则曲线![]() 是平面
是平面![]() 内的双曲线.
内的双曲线.
(3)解:在如图所示的![]() 的坐标系中,因为
的坐标系中,因为![]() 、
、![]() 、
、![]() ,设
,设![]() .则有
.则有![]() ,故
,故![]() 的方程为
的方程为![]() ,
,
代入双曲线![]() :
:![]() 的方程可得,
的方程可得,![]() ,其中
,其中![]() .
.
因为直线![]() 与双曲线
与双曲线![]() 交于点
交于点![]() ,故
,故![]() .进而可得
.进而可得![]() ,即
,即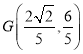 .故双曲线
.故双曲线![]() 在直角梯形
在直角梯形![]() 内部(包括边界)的区域满足
内部(包括边界)的区域满足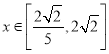 ,
,![]() .又设
.又设![]() 为双曲线
为双曲线![]() 上的动点,
上的动点,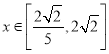 .
.
所以,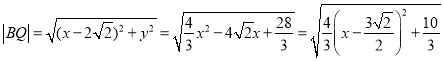
因为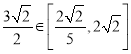 ,所以当
,所以当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
而要使圆![]() 与
与![]() 、
、![]() 都有交点,则
都有交点,则![]() .
.
故满足题意的圆的半径取值范围是 .
.
因为![]() ,所以
,所以![]() 体积为
体积为![]() .故问题可以转化为研究
.故问题可以转化为研究![]() 的面积.又因为
的面积.又因为![]() 为直角,所以
为直角,所以![]() 必为等腰直角三角形.
必为等腰直角三角形.
由前述,设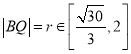 ,则
,则![]() ,
,
故其面积![]() ,所以
,所以![]() .
.
于是,![]() .
.
(当![]() 点运动到与点
点运动到与点![]() 重合时,体积取得最大值;当
重合时,体积取得最大值;当![]() 点运动到横坐标
点运动到横坐标![]() 时,即
时,即![]() 长度最小时,体积取得最小值)
长度最小时,体积取得最小值)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目