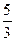题目内容
((本小题满分12分)
已知数列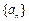 是公差为
是公差为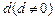 的等差数列,
的等差数列,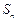 为其前
为其前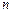 项和。
项和。
(1)若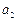 ,
,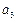 ,
,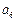 依次成等比数列,求其公比
依次成等比数列,求其公比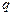 ;
;
(2)若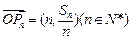 ,求证:对任意的
,求证:对任意的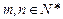 ,向量
,向量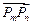 与向量
与向量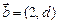 共线;
共线;
(3)若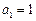 ,
,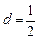 ,
,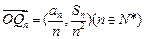 ,问是否存在一个半径最小的圆,使得对任意的
,问是否存在一个半径最小的圆,使得对任意的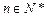 ,点
,点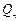 都在这个圆内或圆周上。
都在这个圆内或圆周上。
已知数列
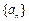 是公差为
是公差为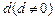 的等差数列,
的等差数列,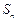 为其前
为其前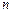 项和。
项和。(1)若
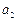 ,
,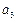 ,
,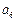 依次成等比数列,求其公比
依次成等比数列,求其公比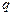 ;
;(2)若
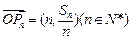 ,求证:对任意的
,求证:对任意的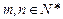 ,向量
,向量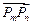 与向量
与向量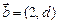 共线;
共线;(3)若
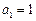 ,
,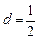 ,
,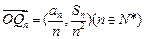 ,问是否存在一个半径最小的圆,使得对任意的
,问是否存在一个半径最小的圆,使得对任意的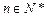 ,点
,点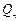 都在这个圆内或圆周上。
都在这个圆内或圆周上。解:(1)因为
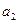 ,
,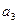 ,
,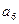 成等比数列,所以
成等比数列,所以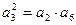 ,
,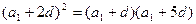 。
。
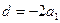 ,
,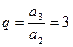 。
。(2)因为
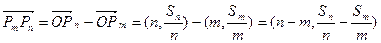 ,而
,而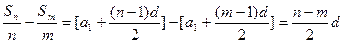 ,
,所以
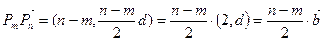 ,所以向量
,所以向量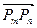 与向量
与向量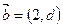 共线。
共线。(3)因为
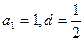 ,所以
,所以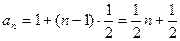 ,
,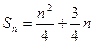 。
。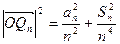
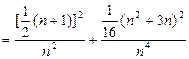
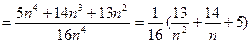
=
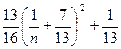 。
。因为
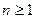 ,所以
,所以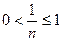 。
。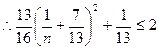 ,当
,当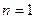 时取等号。
时取等号。所以
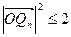 ,即
,即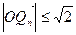 所以存在半径最小的圆,最小半径为
所以存在半径最小的圆,最小半径为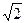 ,
,使得对任意的
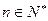 ,点
,点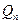 都在这个圆内或圆周上。
都在这个圆内或圆周上。略

练习册系列答案
相关题目
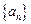 中,
中,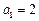 ,
,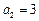 ,其前
,其前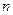 项和
项和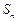 满足
满足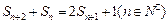 ;数列
;数列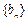 中,
中,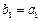 ,
,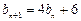
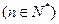 .
.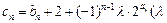 为非零整数,
为非零整数,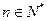 ),试确定
),试确定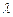 的值,使得对任意
的值,使得对任意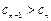 成立.
成立.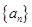 的公差大于0,且
的公差大于0,且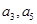 是方程
是方程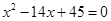 的两根,数列
的两根,数列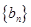 的前
的前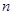 项的和为
项的和为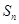 ,且
,且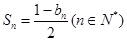 .
.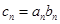 ,求数列
,求数列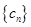 的前
的前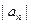 ,
,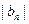 中,a1=2,b1=4,且
中,a1=2,b1=4,且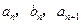 成等差数列,
成等差数列,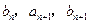 成等比数列(
成等比数列(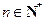 )
) 2,b3,b4,由此猜测
2,b3,b4,由此猜测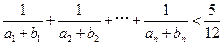 .
.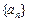 的公比大于1,
的公比大于1,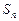 是数列
是数列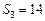 ,且
,且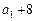 ,
,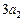 ,
,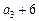 依次成等差数列,数列
依次成等差数列,数列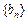 满足:
满足: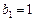 ,
,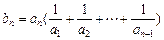
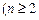 )
)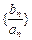 的前n项和为
的前n项和为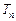
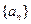 的前6项和为
的前6项和为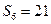 ,且
,且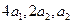 成等差数列,则
成等差数列,则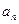 =" " ( )
=" " ( )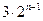
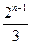
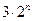
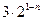
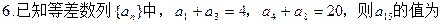
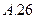
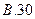
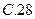
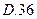
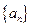 中,已知
中,已知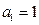 ,
,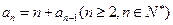 ,则
,则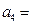 ___________.
___________.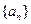 的前n项和为
的前n项和为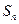 ,且
,且 ,则
,则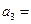 ( )
( )