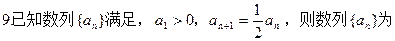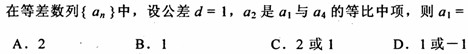题目内容
(本小题满分12分)
已知数列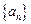 中,
中,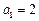 ,
,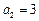 ,其前
,其前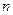 项和
项和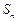 满足
满足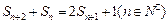 ;数列
;数列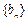 中,
中,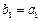 ,
,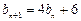
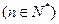 .
.
(1)求数列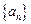 、
、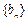 的通项公式;
的通项公式;
(2)设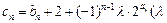 为非零整数,
为非零整数,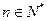 ),试确定
),试确定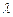 的值,使得对任意
的值,使得对任意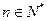 ,都有
,都有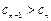 成立.
成立.
已知数列
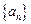 中,
中,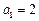 ,
,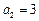 ,其前
,其前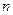 项和
项和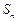 满足
满足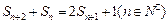 ;数列
;数列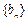 中,
中,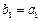 ,
,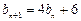
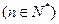 .
.(1)求数列
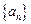 、
、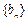 的通项公式;
的通项公式;(2)设
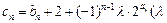 为非零整数,
为非零整数,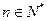 ),试确定
),试确定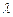 的值,使得对任意
的值,使得对任意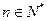 ,都有
,都有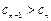 成立.
成立.(1)由已知,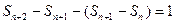
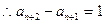 (
(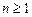 )
)
又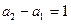 2分
2分
∴数列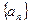 是以
是以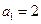 为首项,公差为1的等差数列.
为首项,公差为1的等差数列.
∴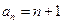 3分
3分
又
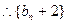 是以4为公比,4为首项的等比数列
是以4为公比,4为首项的等比数列
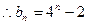 6分
6分
(2)∵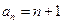 ,
,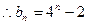 ∴
∴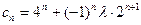 ,
,
要使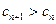 恒成立,
恒成立,
∴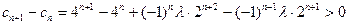
恒成立,∴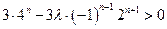 恒成立,
恒成立,
∴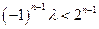 恒成立. 8分
恒成立. 8分
(ⅰ)当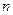 为奇数时,即
为奇数时,即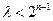 恒成立,
恒成立,
当且仅当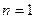 时,
时,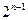 有最小值为1,
有最小值为1,
∴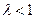 10分
10分
(ⅱ)当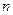 为偶数时,即
为偶数时,即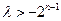 恒成立,
恒成立,
当且仅当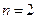 时,
时,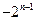 有最大值
有最大值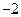 ,∴
,∴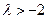 1
1 1分
1分
即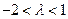 ,又
,又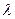 为非零整数,则
为非零整数,则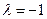 .
.
综上所述,存在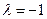 ,使得对任意
,使得对任意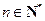 ,都有
,都有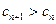 . 12分
. 12分
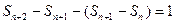
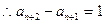 (
(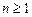 )
)又
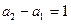 2分
2分∴数列
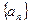 是以
是以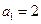 为首项,公差为1的等差数列.
为首项,公差为1的等差数列.∴
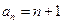 3分
3分又

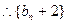 是以4为公比,4为首项的等比数列
是以4为公比,4为首项的等比数列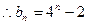 6分
6分(2)∵
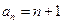 ,
,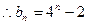 ∴
∴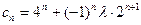 ,
,要使
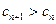 恒成立,
恒成立,∴
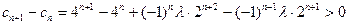
恒成立,∴
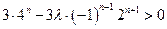 恒成立,
恒成立,∴
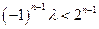 恒成立. 8分
恒成立. 8分(ⅰ)当
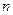 为奇数时,即
为奇数时,即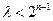 恒成立,
恒成立,当且仅当
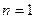 时,
时,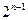 有最小值为1,
有最小值为1,∴
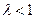 10分
10分(ⅱ)当
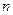 为偶数时,即
为偶数时,即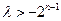 恒成立,
恒成立,当且仅当
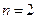 时,
时,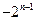 有最大值
有最大值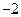 ,∴
,∴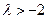 1
1 1分
1分即
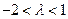 ,又
,又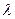 为非零整数,则
为非零整数,则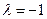 .
.综上所述,存在
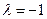 ,使得对任意
,使得对任意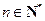 ,都有
,都有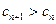 . 12分
. 12分略

练习册系列答案
相关题目
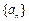 是公差为
是公差为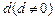 的等差数列,
的等差数列,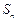 为其前
为其前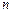 项和。
项和。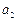 ,
,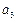 ,
,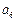 依次成等比数列,求其公比
依次成等比数列,求其公比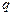 ;
;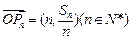 ,求证:对任意的
,求证:对任意的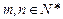 ,向量
,向量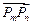 与向量
与向量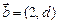 共线;
共线;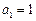 ,
,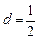 ,
,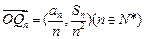 ,问是否存在一个半径最小的圆,使得对任意的
,问是否存在一个半径最小的圆,使得对任意的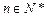 ,点
,点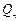 都在这个圆内或圆周上。
都在这个圆内或圆周上。 的前n项和
的前n项和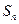 满足
满足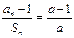 (a>0,且
(a>0,且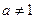 )。数列
)。数列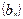 满足
满足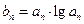
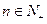 都有
都有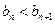 ,求a的取值范围。
,求a的取值范围。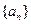 的前5项之和
的前5项之和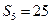 ,且
,且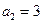 ,则
,则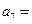 ( )
( )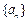 的前
的前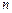 项和为
项和为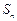 ,且满足
,且满足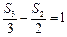 ,则数列
,则数列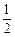
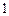

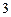
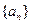 中,
中,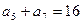 ,
,
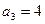 ,则
,则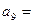 ( )
( )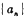 中,
中,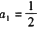 ,点
,点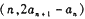 在直线y = x上,其中n = 1,2,3,….
在直线y = x上,其中n = 1,2,3,….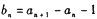 ,证明数列
,证明数列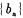 是等比数列;
是等比数列;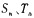 分别为数列
分别为数列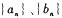 的前n项和,证明数列
的前n项和,证明数列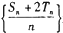 是等差数列
是等差数列