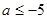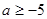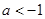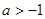题目内容
若函数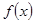 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意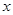 ,恒有
,恒有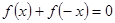 ②对于定义域上的任意
②对于定义域上的任意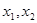 ,当
,当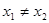 时,恒有
时,恒有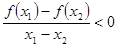 ,则称函数
,则称函数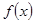 为
为
“理想函数”。给出下列四个函数中:⑴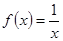 ⑵
⑵ 
 ⑶
⑶ 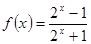
⑷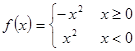 ,能被称为“理想函数”的有_ _ (填相应的序号) 。
,能被称为“理想函数”的有_ _ (填相应的序号) 。
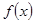 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意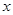 ,恒有
,恒有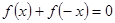 ②对于定义域上的任意
②对于定义域上的任意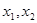 ,当
,当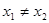 时,恒有
时,恒有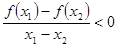 ,则称函数
,则称函数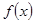 为
为“理想函数”。给出下列四个函数中:⑴
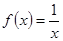 ⑵
⑵ 
 ⑶
⑶ 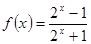
⑷
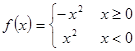 ,能被称为“理想函数”的有_ _ (填相应的序号) 。
,能被称为“理想函数”的有_ _ (填相应的序号) 。(4)
依题意,性质①反映函数f(x)为定义域上的奇函数,性质②反映函数f(x)为定义域上的单调减函数,
⑴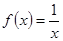 为定义域上的奇函数,但不是定义域上的单调减函数,其单调区间为(-∞,0),(0,+∞),故排除(1);
为定义域上的奇函数,但不是定义域上的单调减函数,其单调区间为(-∞,0),(0,+∞),故排除(1);
⑵ 为定义域上的偶函数,排除(2);
为定义域上的偶函数,排除(2);
 ⑶
⑶ 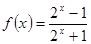 定义域为R,由于y=2x+1在R上为增函数,故函数f(x)为R上的增函数,排除(3);
定义域为R,由于y=2x+1在R上为增函数,故函数f(x)为R上的增函数,排除(3);
⑷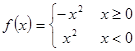 ,的图象如图:
,的图象如图:
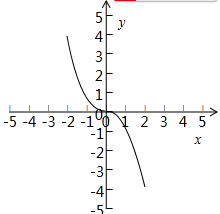
显然此函数为奇函数,且在定义域上为减函数,故(4)为理想函数故答案为 (4)
⑴
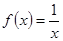 为定义域上的奇函数,但不是定义域上的单调减函数,其单调区间为(-∞,0),(0,+∞),故排除(1);
为定义域上的奇函数,但不是定义域上的单调减函数,其单调区间为(-∞,0),(0,+∞),故排除(1);⑵
 为定义域上的偶函数,排除(2);
为定义域上的偶函数,排除(2); ⑶
⑶ 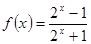 定义域为R,由于y=2x+1在R上为增函数,故函数f(x)为R上的增函数,排除(3);
定义域为R,由于y=2x+1在R上为增函数,故函数f(x)为R上的增函数,排除(3);⑷
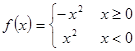 ,的图象如图:
,的图象如图:
显然此函数为奇函数,且在定义域上为减函数,故(4)为理想函数故答案为 (4)

练习册系列答案
相关题目
 若
若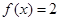 ,则
,则 .
.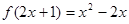 ,则
,则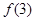 = .
= . 

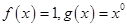


 ,建立集合A到集合B的映射
,建立集合A到集合B的映射 ,
, ,
,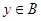 .
. 表达的意义一致的为 ( )
表达的意义一致的为 ( )
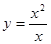
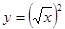

 中,
中,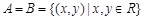 ,且
,且 ,则与A中的元素
,则与A中的元素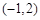 对应的B中的元素为( ).
对应的B中的元素为( ).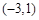
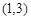
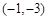
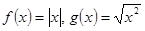
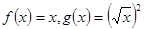
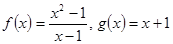

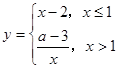 在R上单调递增,则实数
在R上单调递增,则实数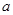 的取值范围是 ( )
的取值范围是 ( )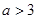
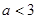
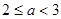
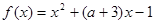 在
在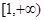 上是增函数,则
上是增函数,则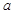 的取值范围是( )
的取值范围是( )