题目内容
【题目】如图所示,在直三棱柱![]() ,其中P为棱
,其中P为棱![]() 上的任意一点,设平面PAB与平面
上的任意一点,设平面PAB与平面![]() 的交线为QR.
的交线为QR.

(1)求证:AB∥QR;
(2)若P为棱![]() 上的中点,求几何体
上的中点,求几何体![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】
(1)由![]() 可得AB//平面
可得AB//平面![]() ,利用线面平行性质定理可得结果;(2)由题意先明确
,利用线面平行性质定理可得结果;(2)由题意先明确![]() 平面
平面![]() ,利用割补法求体积:几何体QR-ABC的体积为
,利用割补法求体积:几何体QR-ABC的体积为![]() .
.
(1)在直三棱柱![]() 中,
中,
因为![]() ,
,![]() 平面
平面![]() .
.![]() 平面
平面![]() ,
,
所以AB//平面![]() .
.
因为平面PAB与平面![]() 的交线为QR,且
的交线为QR,且![]() 平面PAB,
平面PAB,
所以AB∥QR.
(2)在侧面![]() 中,因为BC=2,
中,因为BC=2,![]() ,P为棱
,P为棱![]() 上的中点,
上的中点,
所以![]() ,
,
所以![]() =∠PBC,所以
=∠PBC,所以![]() ,
,
即![]() .
.
在直三棱柱![]() 中,
中,![]() 平面ABC,
平面ABC,
所以![]() .
.
因为AB=BC=2,AC=![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为BC=2,![]() .
.
所以![]()
又![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 。
。
所以![]() .
.
所以几何体QR-ABC的体积为
![]() ,
,
法二:在侧面![]() 中,因为BC=2,
中,因为BC=2,![]() 为棱
为棱![]() 上的中点,
上的中点,
则![]() .
.
所以有![]() ,
,
所以![]() ,
,
则QR,RP,RC三线相互垂直.
又![]() .
.
在△BPC中,由射影定理,可得![]()
在△ABP中,由三角形相似,可得![]()
则![]() .
.
又![]() .
.
则![]()

【题目】某企业生产一种产品,质量测试分为:指标不小于90为一等品,不小于80小于90为二等品,小于80为三等品,每件一等品盈利50元,每件二等品盈利30元,每件三等品亏损10元,现对学徒工甲和正式工人乙生产的产品各100件的检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 | 5 | 15 | 35 | 35 | 7 | 3 |
乙 | 3 | 7 | 20 | 40 | 20 | 10 |
根据上表统计得到甲、乙生产产品等级的频率分别估计为他们生产产品等级的概率.
(1)求出乙生产三等品的概率;
(2)求出甲生产一件产品,盈利不小于30元的概率;
(3)若甲、乙一天生产产品分别为40件和30件,估计甲、乙两人一天共为企业创收多少元?
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 6 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2020年该地区农村居民家庭人均纯收入约为多少千元?
附:回归直线的斜率和截距的最小二乘估计公式分别为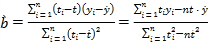 ,
,![]() .
.