题目内容
已知函数f(x)=|log2x|,正实数m、n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m+n等于( )
| A.-1 | B.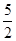 | C.1 | D.2 |
B
由函数f(x)=|log2x|的图象知,
当m<n且f(m)=f(n),得mn=1,且0<m<1<n.
∴0<m2<m<1<n.
∵f(x)在区间[m2,n]上的最大值为2,
∴|log2m2|=2,
∴m=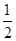 ,n=2,
,n=2,
∴m+n=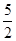 .
.
当m<n且f(m)=f(n),得mn=1,且0<m<1<n.
∴0<m2<m<1<n.
∵f(x)在区间[m2,n]上的最大值为2,
∴|log2m2|=2,
∴m=
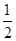 ,n=2,
,n=2,∴m+n=
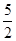 .
.
练习册系列答案
相关题目
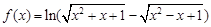 的值域为 .
的值域为 . (x>0,x∈R),下列命题正确的是________.(填序号)
(x>0,x∈R),下列命题正确的是________.(填序号) a=
a= b,下列五个关系式:
b,下列五个关系式: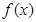 为奇函数,当
为奇函数,当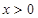 时,
时,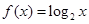 ,则满足不等式
,则满足不等式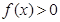 的
的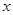 的取值范围是 .
的取值范围是 . <0.如果f
<0.如果f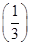 =
= ,4f(
,4f( )>3,那么x的取值范围为( )
)>3,那么x的取值范围为( )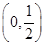
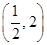
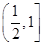 ∪(2,+∞)
∪(2,+∞)  ∪
∪ ,若
,若 ,则
,则 _________.
_________.