题目内容
已知函数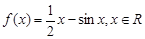 .
.
(1)试求函数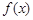 的递减区间;
的递减区间;
(2)试求函数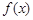 在区间
在区间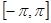 上的最值.
上的最值.
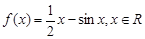 .
.(1)试求函数
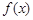 的递减区间;
的递减区间;(2)试求函数
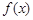 在区间
在区间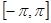 上的最值.
上的最值.(I) ;(2)最大值为
;(2)最大值为 ,最小值为
,最小值为 .
.
 ;(2)最大值为
;(2)最大值为 ,最小值为
,最小值为 .
.试题分析:(1)首先求导函数
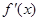 ,然后再通过解不等式
,然后再通过解不等式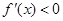 的符号确定单调区间;(2)利用(1)求得极值,然后与
的符号确定单调区间;(2)利用(1)求得极值,然后与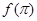 、
、 的值进行比较即可求得最值.
的值进行比较即可求得最值.(I)求导数得:
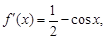
令
 即
即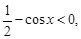 得:
得: ,
,∴函数
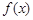 在每个区间
在每个区间 上为减函数.
上为减函数.(2)由(I)知,函数
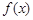 在区间
在区间 上为增函数,在区间
上为增函数,在区间 上为减函数,
上为减函数,∴函数
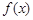 在
在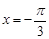 处取极大值
处取极大值 ,在
,在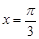 处取极小值
处取极小值 ,
,∵
 ,
, ∴函数
∴函数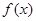 在区间
在区间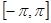 上的最大值为
上的最大值为 ,最小值为
,最小值为 .
.
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
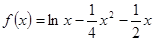 .
.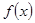 的单调区间和极值;
的单调区间和极值;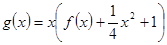 ,当
,当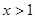 时,
时,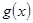 在区间
在区间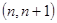 内存在极值,求整数
内存在极值,求整数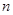 的值.
的值.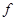 (
(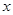 ) =
) =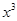 ,g (
,g (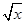 。
。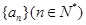 满足
满足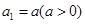 ,
,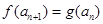 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的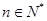 ,都有
,都有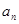 ≤
≤ 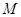 .
.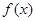 是定义在
是定义在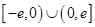 上的奇函数,当
上的奇函数,当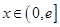 时,
时, 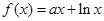 (其中e是自然界对数的底,
(其中e是自然界对数的底,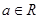 )
)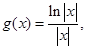 ,求证:当
,求证:当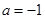 时,且
时,且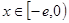 ,
, 恒成立;
恒成立;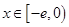 时,
时, ,
,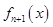 是
是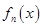 的导函数,即
的导函数,即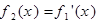 ,
,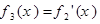 ,…,
,…,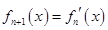 ,
,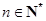 ,则
,则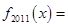 ( )
( )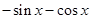
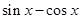
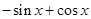
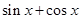
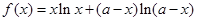
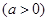 .
.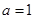 时,求函数
时,求函数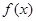 的最小值;
的最小值; ,都有
,都有 ;
;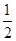 x2(a>0),若对任意两个不等的正实数x1,x2都有
x2(a>0),若对任意两个不等的正实数x1,x2都有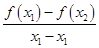 >2恒成立,则a的取值范围是________.
>2恒成立,则a的取值范围是________.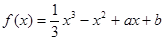 ,
,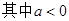 ,如果存在实数
,如果存在实数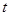 ,使
,使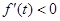 ,则
,则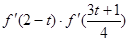 的值( )
的值( )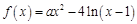 ,
,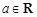 .
.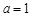 时,求
时,求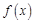 的单调区间;
的单调区间;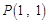 和函数
和函数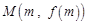 ,对任意
,对任意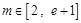 ,直线
,直线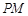 倾斜角都是钝角,求
倾斜角都是钝角,求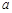 的取值范围.
的取值范围.