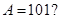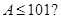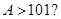题目内容
设函数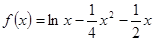 .
.
(1)求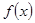 的单调区间和极值;
的单调区间和极值;
(2)若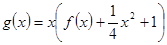 ,当
,当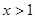 时,
时,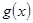 在区间
在区间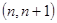 内存在极值,求整数
内存在极值,求整数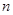 的值.
的值.
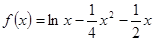 .
.(1)求
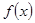 的单调区间和极值;
的单调区间和极值;(2)若
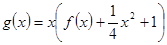 ,当
,当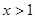 时,
时,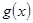 在区间
在区间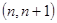 内存在极值,求整数
内存在极值,求整数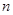 的值.
的值.(1)详见解析;(2)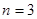 .
.
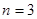 .
.试题分析:(1)此问为导数的基础题型,先求
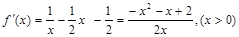 ,令
,令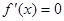 ,求极值点,然后解
,求极值点,然后解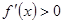 与
与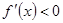 ,列出
,列出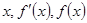 的变化表格,从而很容易确定单调区间,以及极值;
的变化表格,从而很容易确定单调区间,以及极值;(2)代入得到
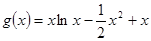 ,先求
,先求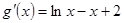 ,从
,从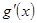 无法确定函数的极值点,所以求其二阶导数,令
无法确定函数的极值点,所以求其二阶导数,令 ,
, 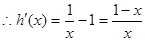 ,当
,当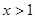 时,
时,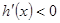 恒成立,
恒成立,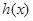 在
在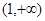 为单调递减函数,那么
为单调递减函数,那么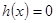 的值为极值点,因为是正整数,所以从
的值为极值点,因为是正整数,所以从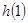 开始判定符号,
开始判定符号,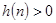 ,
,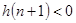 ,即为极值点的区间.
,即为极值点的区间.(1)
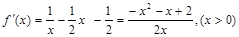 令
令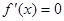 ,解得
,解得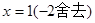 ,
,根据
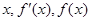 的变化情况列出表格:
的变化情况列出表格: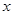 | (0,1) | 1 | 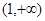 |
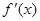 | + | 0 | _ |
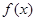 | 递增 | 极大值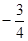 | 递减 |
由上表可知函数
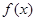 的单调增区间为(0,1),递减区间为
的单调增区间为(0,1),递减区间为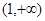 ,
,在
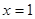 处取得极大值
处取得极大值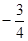 ,无极小值.. 5分
,无极小值.. 5分(2)
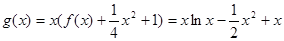 ,
,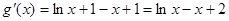 ,
,令
 ,
, 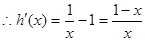 ,
,因为
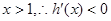 恒成立,所以
恒成立,所以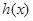 在
在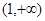 为单调递减函数,
为单调递减函数,因为
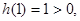
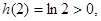
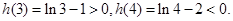
所以
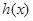 在区间
在区间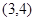 上有零点
上有零点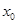 ,且函数
,且函数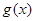 在区间
在区间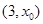 和
和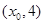 上单调性相反,
上单调性相反,因此,当
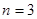 时,
时,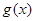 在区间
在区间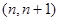 内存在极值.所以
内存在极值.所以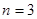 . 12分
. 12分
练习册系列答案
相关题目
 ,
, .
. 的极大值为
的极大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若
,若 关于实数a 可线性分解,求
关于实数a 可线性分解,求 取值范围.
取值范围.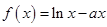 .
.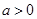 时,求函数
时,求函数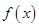 在区间
在区间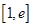 内的最大值;
内的最大值;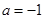 时,方程
时,方程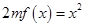 有唯一实数解,求正数
有唯一实数解,求正数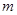 的值.
的值. 在
在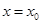 处取最大值。以下各式正确的序号为 .
处取最大值。以下各式正确的序号为 .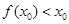 ②
②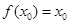 ③
③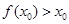 ④
④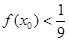 ⑤
⑤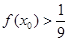
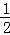 对称,且f′(1)=0
对称,且f′(1)=0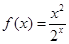 在区间
在区间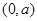 内单调,则
内单调,则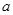 的最大值为__________.
的最大值为__________.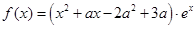 ,其中
,其中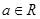 .
.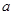 ,使得函数
,使得函数 在
在 上单调递增?若存在,求出的
上单调递增?若存在,求出的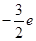 ,求函数的极大值。
,求函数的极大值。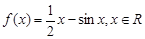 .
.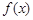 的递减区间;
的递减区间;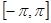 上的最值.
上的最值.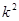 ,若
,若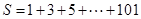 ( )
( )