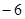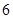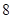题目内容
已知函数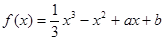 ,
,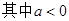 ,如果存在实数
,如果存在实数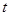 ,使
,使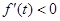 ,则
,则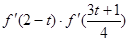 的值( )
的值( )
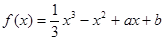 ,
,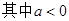 ,如果存在实数
,如果存在实数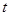 ,使
,使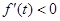 ,则
,则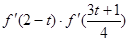 的值( )
的值( )| A.必为正数 | B.必为负数 | C.必为非负 | D.必为非正 |
A
试题分析:∵
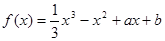 ,∴f′(x)=x2-2x+a.∵存在实数t,使f'(t)<0,a>0,∴t2-2t+a<0的解集不是空集,∴△=4-4a>0,解得a<1,因此0<a<1.令t2-2t+a=0,解得t=1±
,∴f′(x)=x2-2x+a.∵存在实数t,使f'(t)<0,a>0,∴t2-2t+a<0的解集不是空集,∴△=4-4a>0,解得a<1,因此0<a<1.令t2-2t+a=0,解得t=1±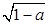 ,∴t2-2t+a<0的解集是{x|0<1?
,∴t2-2t+a<0的解集是{x|0<1?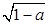 <t<1+
<t<1+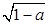 <2}.∵f′(2-t)=(2-t)2-2(2-t)+a=t(t-2)+a,∴f′(2-t)<0;∵
<2}.∵f′(2-t)=(2-t)2-2(2-t)+a=t(t-2)+a,∴f′(2-t)<0;∵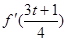 =(
=(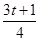 )2?2×
)2?2×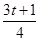 +a=
+a=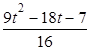 +a,∴f′(t)?f′(
+a,∴f′(t)?f′(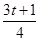 )=t2?2t?
)=t2?2t?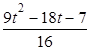 =
= ≥0,∴f′(
≥0,∴f′(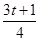 )≤f′(t)<0,∴f′(t+2)•f′(
)≤f′(t)<0,∴f′(t+2)•f′(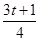 )>0,故选A.
)>0,故选A.
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
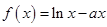 .
.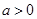 时,求函数
时,求函数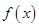 在区间
在区间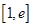 内的最大值;
内的最大值;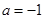 时,方程
时,方程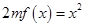 有唯一实数解,求正数
有唯一实数解,求正数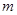 的值.
的值.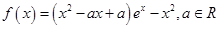 .
.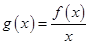 ,当
,当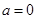 时,讨论
时,讨论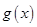 的单调性;
的单调性;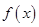 在
在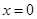 处取得极小值,求
处取得极小值,求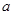 的取值范围.
的取值范围.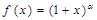 的定义域是
的定义域是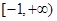 ,其中常数
,其中常数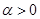 .(注:
.(注: 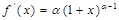
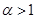 ,求
,求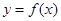 的过原点的切线方程.
的过原点的切线方程.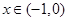 ,恒有
,恒有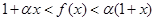 .
.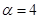 时,求最大实数
时,求最大实数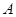 ,使不等式
,使不等式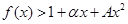 对
对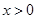 恒成立.
恒成立.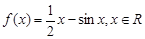 .
.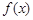 的递减区间;
的递减区间;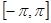 上的最值.
上的最值. (
( ,
, ).
). 时,求曲线
时,求曲线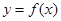 在点
在点 处切线的方程;
处切线的方程; 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.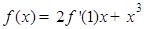 ,则
,则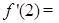 ( )
( )