题目内容
【题目】区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式,2015年至2019年五年期间,中国的区块链企业数量逐年增长,居世界前列现收集我国近5年区块链企业总数量相关数据,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:参考数据![]() (其中z=lny).
(其中z=lny).
附:样本(xi,yi)(i=1,2,…,n)的最小二乘法估计公式为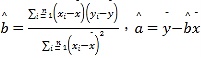
(1)根据表中数据判断,y=a+bx与y=cedx(其中e=2.71828…,为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求y关于x的回归方程(结果精确到小数点后第三位);
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司就获得此次信息化比赛的“优胜公司”,已知在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
【答案】(1)选y=cedx;(2)![]() ;(3)甲与丙两公司进行首场比赛时,甲公司获得“优胜公司”的概率大
;(3)甲与丙两公司进行首场比赛时,甲公司获得“优胜公司”的概率大
【解析】
(1)直接由表中数据可得选择回归方程y=cedx,适宜预测未来几年我国区块链企业总数量;
(2)对y=cedx两边取自然对数,得lny=lnc+dx,转化为线性回归方程求解;
(3)对于首场比赛的选择有以下三种情况:A、甲与乙先赛;B、甲与丙先赛;C、丙与乙先赛,由已知结合互斥事件与相互独立事件的概率计算公式分别求得甲公司获得“优胜公司”的概率得结论.
(1)选择回归方程y=cedx,适宜预测未来几年我国区块链企业总数量;
(2)对y=cedx两边取自然对数,得lny=lnc+dx,
令z=lny,a=lnc,b=d,得z=a+bx.
由于![]() ,
,![]() ,
,![]() ,
,
∵ 0.752,
0.752,
![]() .
.
∴z关于x的回归方程为![]() ,
,
则y关于x的回归方程为![]() ;
;
(3)对于首场比赛的选择有以下三种情况:
A、甲与乙先赛;B、甲与丙先赛;C、丙与乙先赛.
由于在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,
,
则甲公司获胜的概率分别是:
P(A)![]() ;
;
P(B)![]() ;
;
P(C)![]() .
.
由于![]() ,
,
∴甲与丙两公司进行首场比赛时,甲公司获得“优胜公司”的概率大.

 名校课堂系列答案
名校课堂系列答案【题目】某商场为提高服务质量,随机调查了60名男顾客和80名女顾客,每位顾客均对该商场的服务给出满意或不满意的评价,得到下面不完整的列联表:
满意 | 不满意 | 合计 | |
男顾客 | 50 | ||
女顾客 | 50 | ||
合计 |
(1)根据已知条件将列联表补充完整;
(2)能否有![]() 的把握认为男、女顾客对该商场服务的评价有差异?
的把握认为男、女顾客对该商场服务的评价有差异?
附: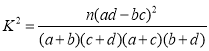
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |