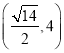题目内容
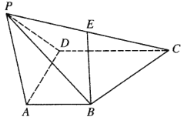
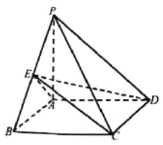
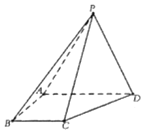
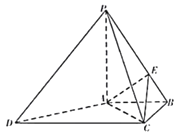
【题目】四棱锥P﹣ABCD中,AB∥CD,AB⊥BC,AB=BC=1,PA=CD=2,PA⊥底面ABCD,E在PB上.
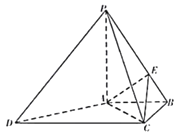
(1)证明:AC⊥PD;
(2)若PE=2BE,求三棱锥P﹣ACE的体积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)过A作AF⊥DC于F,推导出AC⊥DA,AC⊥PA,从而AC⊥平面PAD,由此能求出AC⊥PD.
(2)由VP﹣ACE=VP﹣ABC﹣VE﹣ABC,能求出三棱锥P﹣ACE的体积.
(1)过A作AF⊥DC于F,
因为AB∥CD,AB⊥BC,AB=BC=1,所以CF=DF=AF=1,
所以∠DAC=90°,所以AC⊥DA,
又PA⊥底面ABCD,AC平面ABCD,所以AC⊥PA,
又PA,AD平面PAD,PA∩AD=A,所以AC⊥平面PAD,
又PD平面PAD,∴AC⊥PD.
(2)由PE=2BE,可得VP﹣ACE=VP﹣ABC﹣VE﹣ABC,
所以![]() ,
,![]() ,
,
所以三棱锥P﹣ACE的体积VP﹣ACE=VP﹣ABC﹣VE﹣ABC![]() .
.

【题目】区块链技术被认为是继蒸汽机、电力、互联网之后,下一代颠覆性的核心技术区块链作为构造信任的机器,将可能彻底改变整个人类社会价值传递的方式,2015年至2019年五年期间,中国的区块链企业数量逐年增长,居世界前列现收集我国近5年区块链企业总数量相关数据,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 |
企业总数量y(单位:千个) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:参考数据![]() (其中z=lny).
(其中z=lny).
附:样本(xi,yi)(i=1,2,…,n)的最小二乘法估计公式为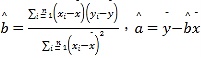
(1)根据表中数据判断,y=a+bx与y=cedx(其中e=2.71828…,为自然对数的底数),哪一个回归方程类型适宜预测未来几年我国区块链企业总数量?(给出结果即可,不必说明理由)
(2)根据(1)的结果,求y关于x的回归方程(结果精确到小数点后第三位);
(3)为了促进公司间的合作与发展,区块链联合总部决定进行一次信息化技术比赛,邀请甲、乙、丙三家区块链公司参赛比赛规则如下:①每场比赛有两个公司参加,并决出胜负;②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛;③在比赛中,若有一个公司首先获胜两场,则本次比赛结束,该公司就获得此次信息化比赛的“优胜公司”,已知在每场比赛中,甲胜乙的概率为![]() ,甲胜丙的概率为
,甲胜丙的概率为![]() ,乙胜丙的概率为
,乙胜丙的概率为![]() ,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
,请通过计算说明,哪两个公司进行首场比赛时,甲公司获得“优胜公司”的概率最大?
【题目】袋子中有四张卡片,分别写有“国”、“富”、“民”、“强”四个字,有放回地从中任取一张卡片,将三次抽取后“国”“富”两个字都取到记为事件A,用随机模拟的方法估计事件A发生的概率,利用电脑随机产生整数0,1,2,3四个随机数,分别代表“国”、“富”、“民”、“强”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
231 | 232 | 210 | 023 | 122 | 021 | 321 | 220 | 031 |
231 | 103 | 133 | 132 | 001 | 320 | 123 | 130 | 233 |
由此可以估计事件A发生的概率为_____.