题目内容
【题目】已知命题![]() 实数
实数![]() 满足
满足![]() (其中
(其中![]() ),命题
),命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(I)若![]() ,且
,且![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)将![]() 代入不等式,并解出命题
代入不等式,并解出命题![]() 中的不等式,同时求出当命题
中的不等式,同时求出当命题![]() 为真命题时实数
为真命题时实数![]() 的取值范围,由条件
的取值范围,由条件![]() 为真命题,可知这两个命题都是真命题,然后将两个范围取交集可得出实数
为真命题,可知这两个命题都是真命题,然后将两个范围取交集可得出实数![]() 的取值范围;
的取值范围;
(Ⅱ)解出命题![]() 中的不等式,由
中的不等式,由![]() 是
是![]() 的必要不充分条件,得出命题
的必要不充分条件,得出命题![]() 中实数
中实数![]() 的取值范围是命题
的取值范围是命题![]() 中不等式解集的真子集,然后列不等式组可求出实数
中不等式解集的真子集,然后列不等式组可求出实数![]() 的取值范围。
的取值范围。
(Ⅰ)由![]() 得
得![]() ,
,
若![]() ,
,![]() 为真时实数t的取值范围是
为真时实数t的取值范围是![]() .
.
由![]() 表示双曲线,得
表示双曲线,得![]() ,即
,即![]() 为真时实数
为真时实数![]() 的取值范围是
的取值范围是![]() .
.
若![]() 为真,则
为真,则![]() 真且
真且![]() 真,所以实数t的取值范围是
真,所以实数t的取值范围是![]()
(Ⅱ)设![]() ,
,
![]() 是
是![]() 的必要不充分条件,
的必要不充分条件,![]() .
.
当![]() 时,
时,![]() ,有
,有![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() ,显然
,显然![]() ,不合题意.
,不合题意.
∴实数a的取值范围是![]() .
.

【题目】据权威部门统计,高中学生眼睛近视已是普遍现象,这与每个学生是否科学用眼有很大关系.每年5月5日是全国爱眼日,我市某中学在此期间开展了一系列的用眼卫生教育活动.为了解本校学生用眼卫生情况,学校医务室随机抽取了100名学生对其进行调查,下面是根据调查结果绘制的学生不间断用眼时间(单位:分钟)的频率分布直方图,且将不间断用眼时间不低于60分钟的学生称为“不爱护眼者”,低于60分钟的学生称为“爱护眼者”.
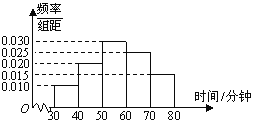
(1)根据频率分布直方图,求这100名学生不间断用眼时间的平均数和中位数(结果精确到0.1);
(2)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“不爱护眼者”与性别有关?
爱护眼者 | 不爱护眼者 | 合计 | |
男 | 45 | ||
女 | 15 | ||
合计 |
(3)在不间断用眼时间为![]() 和
和![]() 两组人中先按分层抽样的方法任意选取5人,再从这5人中随机抽取2人了解他们的视力状况,求这两人来自不同组别的概率.
两组人中先按分层抽样的方法任意选取5人,再从这5人中随机抽取2人了解他们的视力状况,求这两人来自不同组别的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |