Question

【题目】有一块铁皮零件，其形状是由边长为的正方形截去一个三角形所得的五边形，其中，如图所示.现在需要用这块材料截取矩形铁皮，使得矩形相邻两边分别落在上，另一顶点落在边或边上.设，矩形的面积为.

（1）试求出矩形铁皮的面积关于的函数解析式，并写出定义域；

（2）试问如何截取（即取何值时），可使得到的矩形的面积最大？

Answer 1

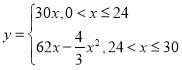【答案】（1），定义域（2）先在DE上截取线段，然后过点M作DE的垂线交BA于点P，再过点P作DE的平行线交DC于点N，最后沿MP与PN截铁皮，所得矩形面积最大.

【解析】

（1）分类讨论,当点分别落在线段或线段上.根据矩形面积即可求得关于的函数解析式及其定义域.

（2）根据（1）由分段函数,结合二次函数的性质可求得面积的最大值.求得取最大值时的值,即可知截取矩形的方式.

（1）依据题意并结合图形,可知：

①当点落在线段上

即时,；

②当点在线段上,

即时,由,

得.

于是.

所以,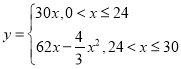

定义域.

（2）由（1）知,当时,；

当时,

当且仅当时,等号成立.

因此,y的最大值为.

答：先在DE上截取线段,然后过点M作DE的垂线交BA于点P,再过点P作DE的平行线交DC于点N,最后沿MP与PN截铁皮,所得矩形面积最大,最大面积为.