题目内容
【题目】已知△ABC的三边长分别为a、b、c,且满足![]() .
.
(1)是否存在边长均为整数的△ABC?若存在,求出三边长;若不存在,说明理由.
(2)若![]() ,
,![]() ,
,![]() ,求出△ABC周长的最小值.
,求出△ABC周长的最小值.
【答案】(1) 存在三边长均为整数的△ABC,其三边长分别为4、5、6或3、7、8. (2) ![]()
【解析】
(1)不妨设![]() ,显然
,显然![]() .
.
若![]() ,此时
,此时![]() .
.
由![]() ,可得
,可得![]() .矛盾.
.矛盾.
故c只能去2、3、4.
当c=2时,![]() ,有
,有![]() .
.
又![]() ,故无解.
,故无解.
当![]() 时,
时,![]() ,即
,即![]() .
.
又![]() ,故
,故![]() 或
或![]() 或
或![]()
解得![]() 或
或![]() 或
或![]()
能构成三角形的只有![]() ,
,![]() ,
,![]() .
.
当![]() 时,同理解得
时,同理解得![]() ,
,![]() 或
或![]() ,
,![]() .
.
而能构成三角形的只有![]() ,
,![]() ,
,![]() .
.
因此,存在三边长均为整数的△ABC,其三边长分别为4、5、6或3、7、8.
(2)由![]() ,
,
得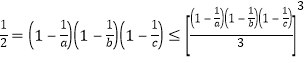
故![]() .
.
又![]() ,
,
则![]() .
.
故△ABC的周长最小值为![]() ,当仅当且
,当仅当且![]() 时,取得此最小值.
时,取得此最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目